На рисунке изображён график линейной функции. Какая из приведённых формул задаёт эту функцию?

y = 3x+1

Пошаговое объяснение:

Каноничное уравнение прямой - y = kx+b, где k и b -коэффициенты
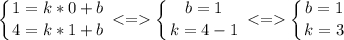
Выделим 2 точки на прямой. Из рисунка видно точки (0;1) и (1;4)
Подставим их координаты в уравнение

Получается уравнение этой прямой будет y = 3x+1

Пошаговое объяснение:

Для того, чтобы проверить какая из формул задаёт график функции, необходимо взять две точки на графике, подставить в формулы координаты х и у этих точек, и проверить, выполняется ли равенство.

Возьмём точки с координатами (0;1) и (1;4) принадлежащие графику.

(0;1):

1=-3*0+1

1=1 - верно.

(1;4):

4=-3*1+1

4=-2 - неверно

⇒ у=-3х+1 - не задаёт график функции.

Известно, что функция у=х задаёт прямую, проходящую через начало координат, нам не подходит.

(0;1):

1=3*0+1

1=1 - верно.

(1;4):

4=3*1+1

4= 4 - верно

⇒ у=3х+1 - задаёт график функции.