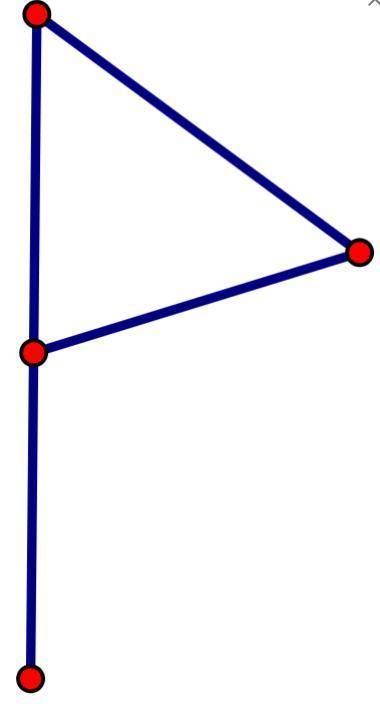
На рисунке изображен граф. Заполните таблицу: а) сколько у него вершин;
б) сколько у него ребер;
в) запишите степени вершин в порядке возрастания через пробел. Например: 1 2 2 4 4 5 5
Другие вопросы по теме Математика
Популярные вопросы
- Найдите наибольший общий делитель чисел 42и70...
3 - Составить приложения из всех слов имели слона, остовляли, ухаживал и за...
2 - Present perfect tense 1) i have cleaned my room. yesterday already now...
1 - Вопросы по рассказу конь с розовой гривой что вы можете сказать о семье...
1 - Периметр четырехугольника 637 см. если длину одной стороны уменьшить на...
1 - Дима за 9 минут 720 м. сколько метров он прлйдёт за 36 минут, если будет...
1 - Даны векторы а(1; 0) и б (1; 1) найдите значение к при котором векторы...
1 - (6m+1)2+(4-12m) при m2=1/12 1/12 - дробь 2 - степень...
3 - Сделать дои 3 читает текст и отвечать на вопросы...
2 - Числитель обычно несократимой дроби на 2 меньше знаменателя если числитель...
3
а) Чтобы определить, сколько у графа вершин, нужно посчитать количество точек на рисунке. По рисунку видно, что у графа 5 вершин.
б) Для определения количества ребер графа нужно посчитать количество линий, соединяющих вершины. При этом нужно быть внимательным и не считать повторные ребра. По рисунку видно, что у графа 7 ребер.
в) Для нахождения степеней вершин нужно посчитать сколько ребер выходит из каждой вершины графа. Для этого вам нужно пройтись по каждой вершине и посчитать количество линий, соединяющих эту вершину с другими вершинами.
Исходя из рисунка, можно определить степени вершин:
1 вершина - 2 ребра выходят из нее;
2 вершина - 3 ребра выходят из нее;
3 вершина - 2 ребра выходят из нее;
4 вершина - 1 ребро выходит из нее;
5 вершина - 1 ребро выходит из нее.
Таким образом, степени вершин графа в порядке возрастания:
1 2 2 3 4 5
Итак, ответы на вопросы:
а) У графа 5 вершин;
б) У графа 7 ребер;
в) Степени вершин графа в порядке возрастания: 1 2 2 3 4 5.