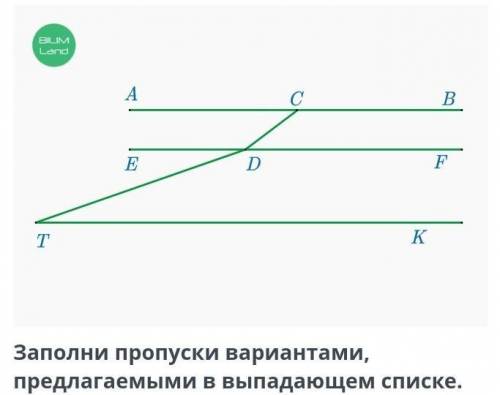
На рисунке ∠DCB = 143°, ∠DTK = 20°, ∠TDF = 160°, ∠TDC = 163°. Заполни пропуски вариантами, предлагаемыми в выпадающем списке.
∠TDE =
.
∠EDC =
.
TK ∥ EF по
признаку параллельности.
AB ∥ EF по
признаку параллельности.​

Давай разберем этот вопрос пошагово.

1. Сначала обратим внимание на угол C. Мы знаем, что TDC = 163°, а ∠DCB = 143°. Сумма углов в треугольнике должна быть равна 180°. Значит, ∠C = 180° - (163° + 143°) = 180° - 306° = -126°. Так как угол не может быть отрицательным, мы можем сказать, что ∠C = 54°.

2. Теперь обратимся к углу D. Мы знаем, что ∠TDC = 163°, а ∠EDC = ? + ∠D. То есть, мы должны вычислить ∠D. Зная, что ∠C = 54°, мы можем найти ∠D = 180° - ∠C = 180° - 54° = 126°. Теперь, зная ∠D, мы можем вычислить ∠EDC = ∠D + ∠C = 126° + 54° = 180°.

3. Следующий угол, который нам нужно найти, - это ∠TDE. Мы знаем, что ∠TDE + ∠EDC = ∠TDC. То есть, ∠TDE = ∠TDC - ∠EDC = 163° - 180° = -17°. Так как угол не может быть отрицательным, мы можем сказать, что ∠TDE = 17°.

4. Наконец, обратимся к параллельным линиям. У нас имеются две пары параллельных линий: TK ∥ EF и AB ∥ EF. Мы знаем, что две линии, пересекаемые третьей линией, и образующие внутри себя соответствующие углы равные, являются параллельными. В данном случае, мы видим, что TK пересекает линии EF и DF. Значит, мы можем сказать, что TK ∥ EF по признаку параллельности. Аналогично, AB пересекает линию EF, поэтому мы можем сказать, что AB ∥ EF по признаку параллельности.

Надеюсь, теперь ответ стал понятен! Если у тебя остались вопросы, не стесняйся задавать их.