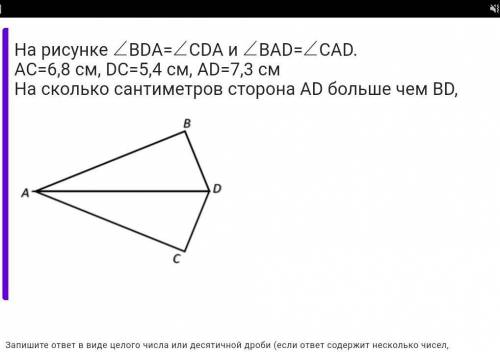
На рисунке∠BDA=∠CDA и∠BAD=∠CAD. AC=6,8 см, DC=5,4 см, AD=7,3 см
На сколько сантиметров сторона AD больше чем BD,
​

Добрый день! Давайте решим эту задачу вместе.

Из условия задачи у нас дано, что ∠BDA=∠CDA и ∠BAD=∠CAD. Это означает, что треугольник ABD и треугольник ACD - подобные треугольники. Подобные треугольники имеют соотношение сторон, пропорциональное соотношению соответствующих углов.

Поэтому, мы можем записать пропорцию сторон AD и BD, используя стороны треугольников ABD и ACD:
AD/BD = AC/DC

Теперь подставим значения сторон AC, DC и AD, которые нам даны в задаче, и решим эту пропорцию:
7,3/BD = 6,8/5,4

Сначала упростим правую часть пропорции, домножив 6,8 и 5,4 на 10 для удобства вычислений:
7,3/BD = 68/54

Теперь сократим доли наибольшим общим делителем чисел 73 и 54:
7,3/BD = 68/54 = 34/27

Чтобы найти BD, нам нужно изолировать его в левой части уравнения, перемножив обе части на BD:
7,3 = (34/27) * BD

Теперь, чтобы найти значение BD, нам нужно разделить число 7,3 на (34/27):
BD = 7,3 / (34/27)

Для деления дроби 7,3 на 34/27, мы можем умножить число 7,3 на обратную дробь 27/34:
BD = 7,3 * (27/34)

Теперь, перемножив числа, получим:
BD = 184,95/34

Выполняем деление:
BD ≈ 5,44 см

Теперь, чтобы найти на сколько сантиметров сторона AD больше, чем сторона BD, вычтем BD из AD:
AD - BD = 7,3 - 5,44

Выполняем вычитание:
AD - BD ≈ 1,86 см

Таким образом, сторона AD больше стороны BD примерно на 1,86 см.