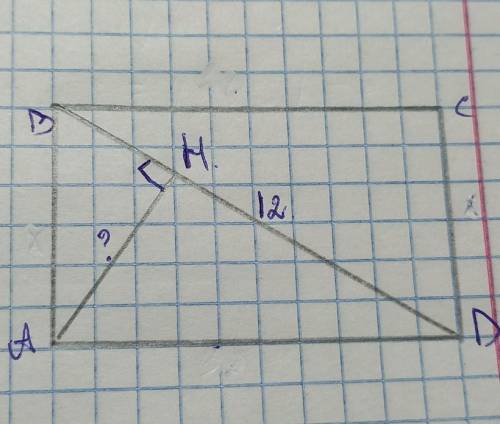
На рисунке ABCD прямоугольник, АH перпендикулярно BD, сторона AB в 3 раза меньше стороны BC . Найдите АН если BC равно 12 см ​

Добрый день!

Для решения данной задачи, нам необходимо воспользоваться информацией о прямоугольнике ABCD.

Из условия задачи известно, что сторона AB в 3 раза меньше стороны BC. Обозначим сторону AB как x, а сторону BC как 3x.

Также известно, что АH является перпендикуляром к BD. Исходя из этого, ты можешь заметить, что прямоугольник ABCD разделен на два равных прямоугольника по вертикали.

Длина стороны АН является высотой одного из этих прямоугольников. Мы можем обозначить ее как h.

Из этой информации, мы можем сформулировать следующее уравнение:

BC = BH + CH

Заменяем значения сторон:

3x = h + h

Складываем h с h, чтобы получить 2h:

3x = 2h

Теперь мы можем выразить h через x:

h = (3/2)x

Таким образом, мы нашли высоту одного из прямоугольников - она равна (3/2)x.

Далее нам нужно найти АН. Мы можем воспользоваться теоремой Пифагора для треугольника АНВ:

(АН)^2 = (АВ)^2 + (ВН)^2

Мы можем сразу заметить, что (ВН) - это h, согласно нашим обозначениям, и (АВ) - это x, так как AB в 3 раза меньше BC.

Таким образом, уравнение преобразуется к следующему виду:

(АН)^2 = x^2 + h^2

Подставляем найденные значения:

(АН)^2 = x^2 + ((3/2)x)^2

(АН)^2 = x^2 + (9/4)x^2

(АН)^2 = (13/4)x^2

Чтобы найти АН, нужно извлечь квадратный корень из обеих сторон:

АН = sqrt((13/4)x^2)

АН = (sqrt(13)x)/2

Таким образом, мы получили выражение для длины АН через сторону AB.