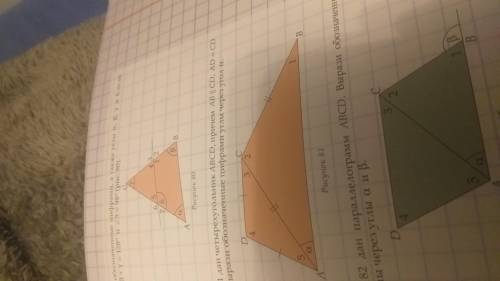
на рисунке 81 дан четырехугольник ABCD,причем AB параллельна CD,AD=CD и AC=BC.Вырази обозначенные цифрами углы через угол a.(РИСУНОК НОМЕР 81)
Другие вопросы по теме Математика
Популярные вопросы
- Рассмотрите календарь сельскохозяйственных работ. Опишите систему сельского...
1 - УМОЛЯЮЮЮЮ Нужно найти значение выражения...
2 - Де зупинився пірат Біллі Бонс...
2 - Образуй, где это возможно, от глаголов страдательные причастия (м. р.,...
1 - Внимательно рассмотри рисунок, на котором указано направление магнитных...
2 - Дана функция: y=4x^4-(3/x^3)+25*(Корень 5 степени)(x^3)+14 Найдите производную...
3 - определите объем углекислого газа(co2), который образуется при взаимодействии...
1 - Use the verbs in the list in the present perfect to complete the sentences....
1 - Решение квадратных уравнений. Урок 3 При каких значениях bуравнение 2у2...
2 - сделать контрольную работу. Буду очень благодарен...
2
ответ: ∠1=α, ∠2=180-2α, ∠3=∠5=α, ∠4=180-2α
Пошаговое объяснение:
ΔABC - равнобедренный ⇒ ∠CAB=∠CBA=∠1=α, тогда
∠2=∠ACB=180 - ∠CAB - ∠CBA=180 - α - α=180 - 2α;
∠DCA=∠CAB=α как внутренние накрест лежащие при ║прямых
ΔADC - равнобедренный ⇒ ∠5=∠CAD=∠3=∠DCA=α;
∠4=∠ADC=180° - ∠DCA - ∠CAD=180°- α - α=180-2α;