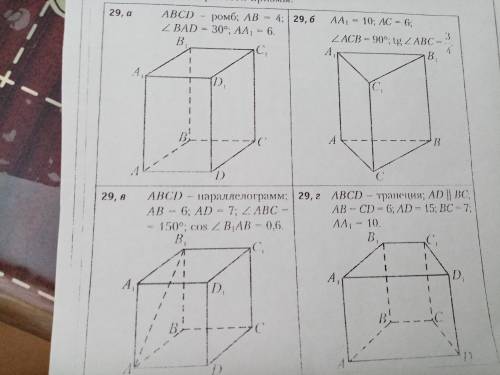
На рисунках 29, а, б, в, г изображена прямая призма. Найдите площадь полной поверхности призмы

Для нахождения площади полной поверхности прямой призмы, нужно сложить площади всех ее граней.

1. Рассмотрим рисунок а:
Если обратить внимание на грани призмы, то видно, что у этой призмы имеется основание в форме прямоугольника и две боковые грани в форме прямоугольного треугольника.

Площадь каждой боковой грани можно найти, используя формулу площади прямоугольника: S = a*b, где a и b - стороны треугольника.

На рисунке известна сторона "а" и высота "h" полей. Поэтому площадь каждой боковой грани равна: Sб = (1/2)*a*h.

Площадь обоих боковых граней равна: Sбок = 2*Sб = 2*(1/2)*a*h = a*h.

Теперь рассмотрим площадь основания прямой призмы. На рисунке также известны стороны "b" и "c". Площадь основания прямоугольника равна: Sосн = b*c.

Суммируя площадь обоих боковых граней и площадь основания, получаем площадь полной поверхности призмы: Sпр = 2*a*h + b*c.

2. Рассмотрим рисунок б:
На этом рисунке основание призмы - прямоугольник, а боковые грани также являются прямоугольниками. Площадь каждой боковой грани равна: Sб = a*d, где a и d - стороны прямоугольника.

Площадь обоих боковых граней равна: Sбок = 2*Sб = 2*a*d = 2ad.

Теперь рассмотрим площадь основания прямой призмы. На рисунке известны стороны "b" и "c". Площадь основания прямоугольника равна: Sосн = b*c.

Суммируя площадь обоих боковых граней и площадь основания получаем площадь полной поверхности призмы: Sпр = 2ad + bc.

3. Рассмотрим рисунок в:
На этом рисунке основание призмы - равносторонний треугольник, а боковые грани являются прямоугольниками. Площадь каждой боковой грани равна: Sб = a*b, где a и b - стороны прямоугольника.

Площадь обоих боковых граней равна: Sбок = 2*Sб = 2*a*b = 2ab.

Теперь рассмотрим площадь основания прямой призмы. На рисунке известна сторона "c". Площадь основания треугольника равна: Sосн = (c^2*sqrt(3))/4.

Суммируя площадь обоих боковых граней и площадь основания получаем площадь полной поверхности призмы: Sпр = 2ab + (c^2*sqrt(3))/4.

4. Рассмотрим рисунок г:
На этом рисунке основание призмы - круг, а боковая грань является прямоугольником.

Площадь боковой грани равна: Sб = 2*π*r*h, где r - радиус основания, h - высота призмы.

Площадь основания круга равна: Sосн = π*r^2.

Суммируя площадь боковой грани и площадь основания, получаем площадь полной поверхности призмы: Sпр = 2*π*r*h + π*r^2.

Это позволяет найти площадь полной поверхности прямой призмы для каждого изображенного рисунка а, б, в и г, используя соответствующие формулы и заданные размеры сторон и высоту призмы.