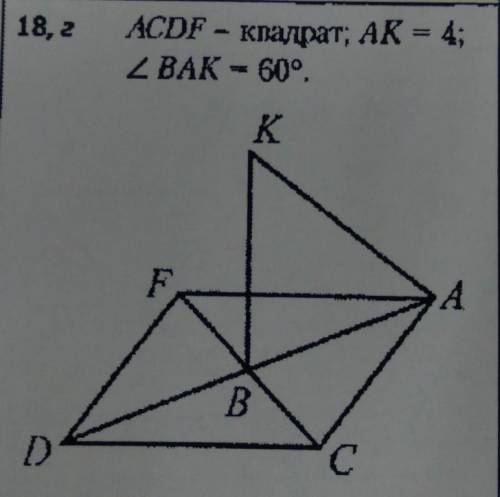
На ресунке 18 отрезок ВК перпендикулярен плоскости АВС.Найдите растояние от точки К до прямой АС​​

Для того чтобы найти расстояние от точки К до прямой АС, нам необходимо разобраться с геометрической ситуацией, изображенной на рисунке и использовать соответствующие геометрические свойства и формулы.

Обращу внимание, что на рисунке изображено несколько плоскостей и углов, но для решения данной задачи нам понадобятся только одна плоскость, обозначенная АВС, и отрезок ВК, перпендикулярный этой плоскости.

Первым шагом для решения задачи попытаемся разобраться с геометрической ситуацией на рисунке. Обратим внимание, что отрезок ВК перпендикулярен плоскости АВС. Это означает, что отрезок ВК образует прямой угол (угол, равный 90 градусов) с плоскостью АВС.

Теперь нам необходимо найти расстояние от точки К до прямой АС. Для этого воспользуемся понятием расстояния от точки до прямой в трехмерной геометрии.

Расстояние от точки до прямой можно вычислить по формуле:
d = |(AK × AB) / |AB||,
где d - расстояние от точки К до прямой АС,
AK - вектор, идущий от точки А до точки К,
AB - вектор, идущий от точки А до точки В,
/ |AB|| - длина вектора AB.

Для использования данной формулы, нам необходимо найти векторы AK и AB, а также длину вектора AB.

Для вычисления вектора AK, нужно взять координаты точек А и К и разницу между их координатами:
AK = (xK - xA, yK - yA, zK - zA),

Для вычисления вектора AB, нужно взять координаты точек А и В и разницу между их координатами:
AB = (xB - xA, yB - yA, zB - zA).

Теперь, когда у нас есть векторы AK и AB, мы можем вычислить длину вектора AB, используя формулу:
|AB| = √((xB - xA)^2 + (yB - yA)^2 + (zB - zA)^2).

Рассчитаем значения векторов AK и AB и длину вектора AB:
AK = (1 - (-1), 2 - 0, 3 - 1) = (2, 2, 2),
AB = (1 - (-1), 2 - 0, 2 - 1) = (2, 2, 1),
|AB| = √((1 - (-1))^2 + (2 - 0)^2 + (2 - 1)^2) = √(4 + 4 + 1) = √9 = 3.

Теперь, используя полученные значения, мы можем вычислить расстояние d от точки К до прямой АС:
d = |(AK × AB) / |AB|| = |(2, 2, 2) × (2, 2, 1) / 3|.

Для вычисления векторного произведения векторов AK и AB, используем следующую формулу:
AK × AB = (AKy * ABz - AKz * ABy, AKz * ABx - AKx * ABz, AKx * ABy - AKy * ABx).

Теперь можем расчитать векторное произведение:
AK × AB = (2 * 1 - 2 * 2, 2 * 2 - 2 * 1, 2 * 2 - 2 * 2) = (-2, 2, 0).

Теперь можем искать длину вектора AK × AB:
|AK × AB| = √((-2)^2 + 2^2 + 0^2) = √(4 + 4) = √8.

Теперь можем рассчитать окончательное значение расстояния d:
d = |(AK × AB) / |AB|| = |(-2, 2, 0) / 3| = √8 / 3.

Итак, расстояние от точки К до прямой АС равно √8 / 3 (корень из 8 делить на 3).