На прямой отмечено несколько точек. петя проделывает с ними операцию удвоения: между любыми двумя соседними точками рисует по точке. после того, как петя проделал операцию удвоения n раз, на прямой оказалось 193 точки. какое наибольшее значение может принимать n?
Другие вопросы по теме Математика
Популярные вопросы
- Vocabulary A Match the part of the words. 6x1/6 (составить словосочетание и перевести...
3 - В каких пластидах происходит фотосинтес? В каких пластидах накапливаются питательные...
2 - Написать сочинение описание по фотографии...
2 - 1. Жаз бен күз айларын салыстыр. Кестені толтыр....
3 - Опишите настроение и желание лирического героя. Раскрой его образ.Зимнее утро...
1 - Рис 333 дано ао 10 co 12 do 6 bo 8 sbod 14 без синусов и косинусов...
3 - Какие слова пропущены в тексте? Впишите наместе пропусков соответствующие цифры...
1 - История мировых цивилизаций как наука и учебная дисциплина. Российская средневековая...
1 - AI+NAOH гидроксид натрия + алюминий...
3 - мне, надо ответить на вопросы 1, 6, 9, 13. Будьте добры какие есть а то меня убьют...
3
Заметим, что если у нас в какой-то момент времени на прямой оказалось точек, то после "удвоения" точек станет ровно
точек, то после "удвоения" точек станет ровно 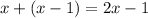 .
.
То есть, чтобы узнать, сколько точек было до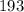 точек, нужно решить уравнение
точек, нужно решить уравнение 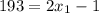 . Понятно, что
. Понятно, что 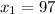 .
.
Узнаем, сколько точек было до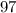 :
: 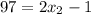 . Здесь
. Здесь 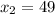 .
.
Очередным уравнением будет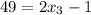 и
и 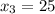 .
.
Далее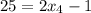 , откуда
, откуда 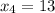 .
.
По аналогии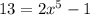 , и, конечно
, и, конечно 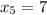 .
.
И, заключительный шаг,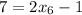 , где
, где 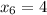 .
.
А уравнение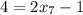 имеет ненатуральный корень
имеет ненатуральный корень  , точек на количество прямой не может быть дробным числом.
, точек на количество прямой не может быть дробным числом.
Получаем, что максимальное значение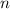 равно
равно 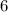 :
:
То есть, больше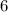 шагов нельзя сделать, иначе бы число точек на прямой было бы дробным.
шагов нельзя сделать, иначе бы число точек на прямой было бы дробным.
ответ: