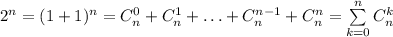На окружности взята 101 точка.сколько существует вписанных в окружность выпуклых многоугольников с вершинами в этих точках?
Другие вопросы по теме Математика
Популярные вопросы
- Под действием силы 50кН тело массой 3 кг изменило свою скорость...
2 - Оценочный вопрос по содержанию текста...
2 - Решите УРОВНЕНИЕ (12цел5/13+Y)9цел9/13=7цел7/13ЦЕЛ:ЭТО ЦЕЛОЕ...
3 - Построить треугольники со сторонами 8,9,10 5,4,3 6,7,2 см вписать...
1 - В каких предложениях НЕ надо ставить запятую (-ые)? * Дневальный...
3 - Скоротити дроби,використовуючи ознаки подільності 10/25 , 8/12...
3 - с этими заданиями. СОР по праву. заранее большое ...
2 - Деректі және өз білімдеріңізді пайдаланып, 20-30 жылдардағы қуғын-сүргіннің...
2 - Зберними есть все именники в рядку А) кориння, брюки, мишваБ)...
1 - Составьте выражение для вычисления площади фигуры изображённой...
2
Пошаговое объяснение:
Количество построить k-угольник по 101 точке -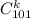 .
.
Тогда количество построить все многоугольники:
Исходя из