На множестве A задано бинарное отношение R. Указать элементы отношения R, записать матрицу отношения R, определить, является ли R отношением эквивалентности.
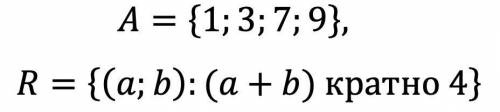
Другие вопросы по теме Математика
Популярные вопросы
- Впервой команде на 14 человек больше,чем во второй.сколько человек...
3 - 2. брусок, маса якого дорівнює 200 г, притискають до вертикальної...
3 - Сочинение по 6 класс 50 слов про маму кулинара...
3 - За столом сидели 2 дочки, 2 матери и 1 бабушка...
1 - Дуже потрі! установіть відповідність між авітамінозом і назвою...
1 - Килограмм конфет косолапый мишка стоит 57,25 (10 система счисления),...
2 - Трое учеников отправились в магазин покупать книгу. первому для...
1 - Отличия 1 и 2 азовского похода(петр 1)...
1 - Как найти сторону треугольника имея только градусы углов? (теорему...
3 - Сумма двух чисел равна 210. наибольшее число на 21 единицу больше...
1
В матричной форме бинарное отношение R можно записать с помощью матрицы, размерность которой равна количеству элементов в множестве A. В данном случае, размерность матрицы будет 5х5. Значение элемента матрицы Rij равно 1, если пара (ai, aj) принадлежит отношению R, и 0 в противном случае.
Теперь рассмотрим данную таблицу и определим элементы отношения R:
(a, a) - элементы на главной диагонали, значение 1. В данном случае, первый элемент a принадлежит отношению R.
(b, b) - элементы на главной диагонали, значение 1. В данном случае, второй элемент b принадлежит отношению R.
(c, c) - элементы на главной диагонали, значение 1. В данном случае, третий элемент c принадлежит отношению R.
(d, d) - элементы на главной диагонали, значение 1. В данном случае, четвертый элемент d принадлежит отношению R.
(e, e) - элементы на главной диагонали, значение 1. В данном случае, пятый элемент e принадлежит отношению R.
(a, b) - элемент в ячейке с координатами (1, 2), значение 0. В данном случае, первый элемент a не связан с вторым элементом b отношением R.
(a, e) - элемент в ячейке с координатами (1, 5), значение 1. В данном случае, первый элемент a связан с пятым элементом e отношением R.
Таким образом, элементы отношения R на множестве A будут: {(a, a), (b, b), (c, c), (d, d), (e, e), (a, e)}.
Теперь запишем матрицу отношения R. Значение элемента матрицы Rij равно 1, если пара (ai, aj) принадлежит отношению R, и 0 в противном случае. По описанному выше определению, матрица отношения R будет следующей:
1 0 0 0 1
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
Теперь давайте проверим, является ли R отношением эквивалентности. Чтобы отношение было эквивалентностью, оно должно выполнять три условия: рефлексивность, симметричность и транзитивность.
1. Рефлексивность: в отношении R каждая пара элементов (ai, ai) должна принадлежать отношению R. В нашем случае, все элементы на главной диагонали матрицы R равны 1, что означает, что отношение рефлексивно.
2. Симметричность: если пара (ai, aj) принадлежит отношению R, то и пара (aj, ai) также должна принадлежать отношению R. В нашем случае, все элементы матрицы R над главной диагональю равны 0, что означает, что отношение не является симметричным.
3. Транзитивность: если пары (ai, aj) и (aj, ak) принадлежат отношению R, то и пара (ai, ak) также должна принадлежать отношению R. В нашем случае, для всех пар элементов (ai, aj), (aj, ak), пара (ai, ak) не принадлежит отношению R, так как соответствующие элементы в матрице R равны 0. Таким образом, отношение не является транзитивным.
Итак, мы можем заключить, что отношение R, заданное на множестве A, не является отношением эквивалентности.