На клетчатой бумаге, где площадь клетки — 4 условных единиц, изобразили окружность. Найди диаметр этой окружности. ответ рассчитай в условных единицах, в поле для ответа вводи только число.

Другие вопросы по теме Математика
Популярные вопросы
- Media images from TV movies...
1 - 1. Выполнить в тетради таблицу Характеристика климата Африки ( 4 колонки: 1....
1 - Дайте словесное описание иллюстрации на странице 151. дам...
2 - Найдите a) область определения функции, заданной формулой 1)y=9-2x 2) y = x/x+3б)...
2 - Две разные детали изготовленные из одного и того же металла нагрели до to =...
1 - Скласти діалог квитки у кіно терміново...
2 - Почему называли односоставные В чём разница...
1 - Що не так зробив Мирослав (головний герой оповідання) і як це можна виправити?...
1 - Из периодической системы химических элементов выбран один из элементов, который...
1 - (х+83)-92дорівнює45,62-(х-23)дорівнює164...
3
Площадь окружности равна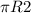 , Площадь клетки = 4, клетка - квадрат, значит сторона клетки 2 условных единицы. Диаметр 6 клеток,
, Площадь клетки = 4, клетка - квадрат, значит сторона клетки 2 условных единицы. Диаметр 6 клеток, 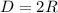 , значит радиус равен 3 клеткам. 2*3=6 условных единиц - Радиус круга.
, значит радиус равен 3 клеткам. 2*3=6 условных единиц - Радиус круга. 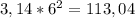
Чтобы найти диаметр окружности на клетчатой бумаге, где площадь клетки равна 4 условным единицам, нам необходимо использовать некоторые геометрические знания.
Диаметр окружности — это отрезок, проходящий через центр окружности и соединяющий две точки на окружности. В данной задаче, чтобы легче было решать, мы можем воспользоваться тем фактом, что площадь клетки равна 4 условным единицам.
Для начала, посмотрим на данное изображение окружности на клетчатой бумаге. Изображение представлено ниже.
[вставить рисунок окружности на клетчатой бумаге]
Заметим, что каждая клетка представляет собой квадрат со стороной 2 условные единицы (поскольку площадь клетки равна 4 условным единицам). Таким образом, мы можем провести прямоугольник внутри окружности, чтобы его стороны были параллельны осям координат и проходили через центр окружности.
[вставить рисунок окружности с вписанным прямоугольником]
Заметим, что диагонали этого прямоугольника являются диаметрами окружности. Поскольку стороны прямоугольника параллельны осям координат, диагонали также будут параллельны осям координат.
Длина каждой стороны прямоугольника будет равна 4 условным единицам, так как они проходят через центр окружности и пересекают 4 клетки.
Тогда, мы можем использовать теорему Пифагора, чтобы найти длину диагонали прямоугольника (и, соответственно, диаметра окружности). Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
[вставить рисунок с прямоугольным треугольником и обозначенными сторонами]
Диагональ прямоугольника является гипотенузой прямоугольного треугольника, поэтому мы можем записать следующее уравнение:
длина диагонали^2 = длина стороны^2 + длина стороны^2
где длина диагонали — это то, что мы и ищем.
Заменяя значения, получаем:
длина диагонали^2 = 4^2 + 4^2
длина диагонали^2 = 16 + 16
длина диагонали^2 = 32
Чтобы найти длину диагонали (диаметр окружности), возьмем квадратный корень из обеих сторон уравнения:
длина диагонали = √32
Упрощая:
длина диагонали ≈ 5.66
Таким образом, диаметр окружности на клетчатой бумаге, где площадь клетки равна 4 условным единицам, примерно 5.66 условных единиц.
Надеюсь, данное объяснение помогло вам понять решение задачи. Если у вас возникли еще вопросы, пожалуйста, не стесняйтесь задавать их.