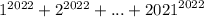
на какую цифру заканчивается?

1^n = 1

2^n: 2,4,8,6

3^n: 3,9,7,1

4^n:4,6,4,6...

5^n:5

6^n:6

7^n:7,9,3,1...

8^n:8,4,2,6..

9^n:9,1,9,1...

у цифр последняя цифра повторяется через 4 варианта, поэтому 2022:4=505 и остаток-2.

значит, n^2022(последняя цифра)=n^2(последняя цифра)

1-9: 1+4+9+6+5+6+9+4+1= 45( нам нужен только 5)

1-99: 5+5+5+5+5+5+5+5+5+5=0

1-1999:0

2000-2020:0

2021^2022:1

0+0+1=1

ответ : последняя цифра-1