На экзамене по есть 4 темы, в которых 7,6,8, 10 вопросов соответственно. студент знает правильные ответы на 6,4,6,7 вопросов. в процессе экзамена ему два случайно выбранных вопроса из разных тем. если студент не отвечает, то считается не сдавшим. мы знаем, что студент не сдал экзамен. какова вероятность что его подвёл вопрос из второй темы.
Другие вопросы по теме Математика
Популярные вопросы
- Решите , развернутым ! 4x-2(x+7)=2(3-x)...
2 - Решите многоэтажные дроби: 1: 2/3 1: 1/7 1: 5/2...
2 - Какой корень у слов ванна аккуратно аппетит класс шоссе чувство солнце...
2 - Перевод my naughty little sister is i ll...
1 - Как решить . расстояния от минска -бреста 348 км. поезд минск -брест...
2 - Напишите 20 предложений тема как развивался человек...
2 - Cалгоритма rle закодируйте сообщение: bbaaa с объяснением,...
2 - Мини сочинение на тему явление в жизни растений надо...
1 - Сput the words in the correct order to make questions and sentences....
2 - 1. запишите, обозначая приставки и расставляя ударения. затрубить, отрубить;...
3
≈ 0.254
Пошаговое объяснение:
Пусть имеются следующие гипотезы:
H₁ - студенту попался вопрос на билет из 1 темы
H₂ - студенту попался вопрос на билет из 2 темы
H₃ - студенту попался вопрос на билет из 3 темы
H₄ - студенту попался вопрос на билет из 4 темы
Соответственно априорные вероятности тогда равны P(H₁)=P(H₂)=P(H₃)=P(H₄) =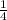
Пусть событие A связано с тем, что студент не ответил на вопрос. Тогда условные вероятности равны:
А полная вероятность (т.е. вероятность того, что студент не сдал экзамен) равна сумме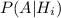 по всем i.
по всем i.
Находим теперь апостериорную вероятность, согласно формуле Байеса:
Таким образом,