На единичной окружности отметьте точку, полученную поворотом точки P(1; 0) на заданный угол: 1) 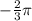$-\frac{2}{3} \pi$

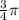
2) $\frac{3}{4}\pi$

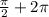
3) $\frac{\pi }{2}+2\pi$

4) $-\pi -2\pi$

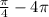
5) $\frac{\pi }{4}-4\pi$

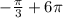
6) $-\frac{\pi }{3} +6\pi$

Ответы

Kok1n 29.12.2023 08:15

Для решения этой задачи, нам необходимо использовать формулу поворота точки на единичной окружности. Данная формула использует тригонометрические функции синус и косинус. Поэтому перед решением задачи, рассмотрим значение синуса и косинуса для основных углов на единичной окружности:

Угол 0:
син(0) = 0,
кос(0) = 1.

Угол π/6:
син(π/6) = 1/2,
кос(π/6) = √3/2.

Угол π/4:
син(π/4) = √2/2,
кос(π/4) = √2/2.

Угол π/3:
син(π/3) = √3/2,
кос(π/3) = 1/2.

Угол π/2:
син(π/2) = 1,
кос(π/2) = 0.

Угол 2π:
син(2π) = 0,
кос(2π) = 1.

Теперь рассмотрим каждый из заданных углов по отдельности:

1) Угол -2/3π:
Для поворота точки P(1; 0) на угол -2/3π, нам необходимо использовать значения синуса и косинуса для этого угла из таблицы:

син(-2/3π) = -√3/2,
кос(-2/3π) = -1/2.

Исходя из этих значений, мы можем найти новые координаты точки, повернутой на заданный угол:

x' = 1*кос(-2/3π) - 0*син(-2/3π) = -1/2,
y' = 1*син(-2/3π) + 0*кос(-2/3π) = -√3/2.

Таким образом, точка, полученная поворотом P(1;0) на угол -2/3π, имеет координаты (-1/2; -√3/2).

2) Угол 3/4π:
Аналогично предыдущему пункту, найдем значения синуса и косинуса для угла 3/4π:

син(3/4π) = -√2/2,
кос(3/4π) = √2/2.

Затем, используем эти значения для вычисления новых координат точки:

x' = 1*кос(3/4π) - 0*син(3/4π) = √2/2,
y' = 1*син(3/4π) + 0*кос(3/4π) = -√2/2.

Точка, полученная поворотом P(1;0) на угол 3/4π, имеет координаты (√2/2; -√2/2).

3) Угол π/2 + 2π:
Для данного угла, представленного в виде суммы π/2 и 2π, мы можем производить угловые повороты, начиная с координат (1;0), не изменяя значений синуса и косинуса. Таким образом, новые координаты точки будут такими же, как и у исходной точки.

Точка, полученная поворотом P(1;0) на угол π/2 + 2π, имеет такие же координаты (1;0) как и P.

4) Угол -π - 2π:
Аналогично предыдущему пункту, для данного угла представленного в виде разности -π и 2π, мы можем просто отразить исходную точку (1;0) относительно начала координат.

Точка, полученная поворотом P(1;0) на угол -π - 2π, будет иметь координаты (-1;0).

5) Угол π/4 - 4π:
Для данного угла, представленного в виде разности π/4 и 4π, мы можем производить угловые повороты, начиная с координат (1;0), не изменяя значений синуса и косинуса. Таким образом, новые координаты точки будут такими же, как и у исходной точки.

Точка, полученная поворотом P(1;0) на угол π/4 - 4π, имеет такие же координаты (1;0) как и P.

6) Угол -π/3 + 6π:
Для данного угла, мы можем использовать значения синуса и косинуса для угла -π/3 из таблицы:

син(-π/3) = -√3/2,
кос(-π/3) = 1/2.

Затем, используем эти значения для вычисления новых координат точки:

x' = 1*кос(-π/3) - 0*син(-π/3) = 1/2,
y' = 1*син(-π/3) + 0*кос(-π/3) = -√3/2.

Таким образом, точка, полученная поворотом P(1;0) на угол -π/3 + 6π, имеет координаты (1/2; -√3/2).

В итоге, ответы на задачу следующие:
1) (-1/2; -√3/2),
2) (√2/2; -√2/2),
3) (1; 0),
4) (-1; 0),
5) (1; 0),
6) (1/2; -√3/2).

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика