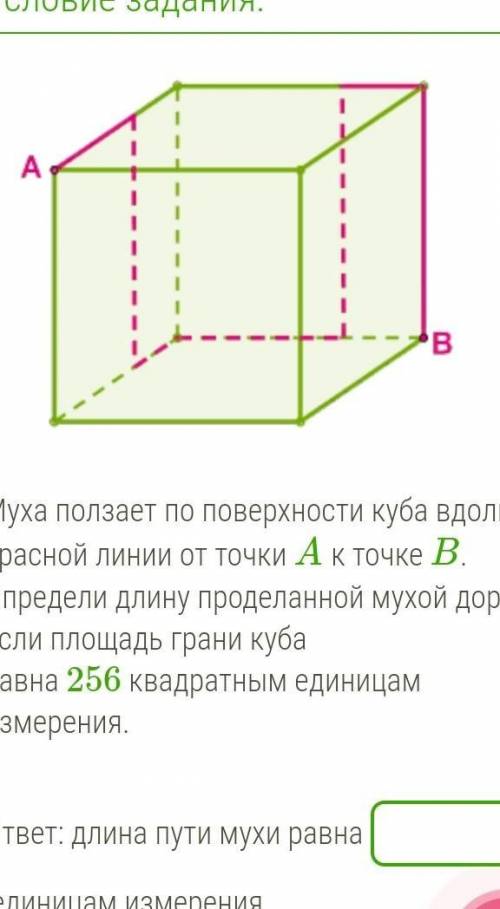
Муха ползает по поверхности куба вдоль красной линии от точки A к точке B. Определи длину проделанной мухой дороги, если площадь грани куба равна 256 квадратным единицам измерения.

 

ответ: длина пути мухи равна  единицам измерения.д​

Для решения этой задачи нам необходимо определить длину пути, который муха проделала по поверхности куба.

Первым шагом, давайте определим, сколько граней есть у куба. Куб состоит из 6 граней: сверху, снизу и на каждой боковой стороне.

Затем, чтобы найти длину пути мухи, мы должны определить, сколько сторон куба она проходит.
Мы видим, что муха проходит только по одной грани, которая имеет красную линию. Остальные грани куба она не использует в своем движении.

Если мы представим куб в виде развёрнутой фигуры, мы увидим, что путь мухи является диагональю этой фигуры.

Для нахождения длины пути, нам необходимо использовать теорему Пифагора.

Вначале, найдем длину стороны куба. Из условия задачи известно, что площадь одной грани составляет 256 квадратных единиц измерения. Поскольку куб имеет 6 граней, каждая сторона куба будет иметь площадь 256 квадратных единиц измерения:

256 квадратных единиц измерения * 6 граней = 1536 квадратных единиц измерения

Теперь найдем длину стороны. Чтобы определить длину каждой стороны, мы должны взять квадратный корень из площади грани:

√(1536 квадратных единиц измерения) = 39 единиц измерения (округленно)

Теперь у нас есть длина стороны куба равная 39 единиц измерения.

Чтобы найти длину пути мухи, нам нужно найти диагональ развернутой фигуры.

Давайте обратимся к фигуре на рисунке. Для простоты, мы можем получить прямоугольный треугольник со сторонами 39, 39 и диагональю, которую мы ищем.

Теперь, применяя теорему Пифагора, получим:

(39 единиц измерения)^2 + (39 единиц измерения)^2 = диагональ^2

39^2 + 39^2 = диагональ^2

1521 единиц измерения + 1521 единиц измерения = диагональ^2

3022 единиц измерения = диагональ^2

Теперь найдем квадратный корень от обеих сторон для получения длины диагонали.

√(3022 единицы измерения) = диагональ

Длина пути мухи равна 55 единицам измерения.

Таким образом, длина пути мухи, проходящей по поверхности куба от точки A до точки B, равна 55 единицам измерения.