1. Математика
  2. Можно решение и ответы (Графики

Можно решение и ответы
(Графики чертить не обязательно)


Можно решение и ответы (Графики чертить не обязательно)

supergirl321 supergirl321    1   20.12.2020 18:10    1

Ответы
yanaerasova017 yanaerasova017  19.01.2021 18:12

А1.

\log_{\frac{1}{3}}x\leq 9\\\\\begin{equation*}\begin{cases}x 0\\x \geq \left(\dfrac{1}{3}\right)^9\end{cases}\end{equation*}\ \ \ \Leftrightarrow\ \begin{equation*}\begin{cases}x 0\\x \geq \dfrac{1}{19683}\end{cases}\end{equation*}\ \ \ \Rightarrow\ \boxed{x\geq \dfrac{1}{19683}}

Знак нижнего неравенства изменился на противоположный с изначальным, поскольку основание логарифма находится в промежутке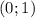 (0; 1).

ответ: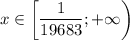  x\in \left[\dfrac{1}{19683};+\infty\right )  .

А2.

а)

y = \log_{4}x + \log_{4}(1-x)

Область определения:

\begin{equation*}\begin{cases}x 0\\1 - x 0\end{cases}\end{equation*}\ \ \ \Leftrightarrow\ \begin{equation*}\begin{cases}x 0\\-x -1\end{cases}\end{equation*}\ \ \ \Leftrightarrow\ \begin{equation*}\begin{cases}x 0\\x < 1\end{cases}\end{equation*}

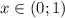ответ: x \in (0;1).

б)

y = \log_{2}(x^2-16)\\\\x^2 - 16 0\\\\(x-4)(x+4) 0

Решим неравенство методом интервалов.

Нули: -4; 4.

         +                          -                           +

-------------------о------------------------о--------------------> x

                    -4                           4

Область определения:

$\left[\begin{gathered}x < -4\\x 4\\\end{gathered}

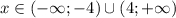ответ: x\in (-\infty; -4)\cup (4; +\infty).

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
SIBGATULLINA98 SIBGATULLINA98  03.10.2019 08:40
1. меркантилизм – это: а) политика государства; б) политика торговой буржуазии; в) политика саморегулирующейся . 2. впервые графически отобразил функциональную зависи-...
anastasijamak anastasijamak  03.10.2019 08:40
Вычисли письменно с проверкой 45078×3 19021×5 273321÷9 147364÷7 69021×4 189009×4 956176÷2 400648÷8...
pchpppr pchpppr  03.10.2019 08:40
Запишите выражения без скобок: 1) m + ( -n ) + p + ( -k ) ; 2) -x + ( -y ) + ( -z ) ; 3) -ab + ( -ac ) + cd ; 4) -a + ( -4c ) + ( -7 ) ; 5) -0,6a + ( -11b ) + 3; 6) 9a...
милаха3451 милаха3451  03.10.2019 08:40
Какие произведения изобразил виктор михайлович васнецов?...
mikiliki889 mikiliki889  03.10.2019 08:40
Какая формула выражает периметр прямоугольника p с длинами сторон 8 дм.и x дм....
musaevakhadizh musaevakhadizh  03.10.2019 08:40
Колесо радиусом 20 см.пройдя некоторое расстояние.сделало 180 оборотов.сколько оборотов при прохождении этого же расстаяния.сделает колесо радиус которого25 см. нужно...
nOMOshHuK2 nOMOshHuK2  03.10.2019 08:40
Сокращается ли дробь ; 128/ 96, 128/75, 125/96, 125/75,...
777alisham 777alisham  03.10.2019 08:40
Как решать уравнения вот такого типа: 5-y/4=3/7...
LinkolnPark1 LinkolnPark1  03.10.2019 08:40
(х+2)^2=(x+4)^2 в ответе укажите больший корень ответ : -3...
HKL11 HKL11  03.10.2019 08:40
Как правельно составить , 2класс. начало вечерней дойки в 5 часов вечера. когда доярке нужно выйти из дома, если на дорогу она тратит 30 минут и надо прийти за 15 минут...

Популярные вопросы