Может кто умеет? нужно найти сумму числового ряда (бесконечноть; n=1) 1/(n^2+9n+18). решите
Другие вопросы по теме Математика
Популярные вопросы
- Номер 31 сократить дроби, пытался искать ответ...
2 - решить задание пацаны и девочки знайти радиус Кола выписать ривностороннього...
2 - Установіть відповідність між прикладами руху тіл та знаками роботи,...
1 - Знаючи що тариф становить 90 копійок за 1 кл/год розрахуйте скільки...
2 - Какой жанр народного творчества напоминает начало Задонщины?...
1 - Определить стоимость электроэнергии потребляемой любым прибором в течении...
1 - Прочитайте текст расскажите что такое там Спишите объясняя написание...
3 - Конспект по литературе на тему предания .11-15 страница.(7 класс Коровин)...
2 - Выполнить синтаксический разбор предложений. Некоторые разновидности...
3 - Встановити відповідність ...
2
Получили, что частичная сумма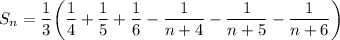 . Переходя к пределу при
. Переходя к пределу при 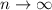 , найдем сумму.
, найдем сумму.
ответ: 37/180.