Могут ли числа корень из 3; 2; корень из 8 быть членами(необязательно последовательными) арифметической прогрессии?
Ответы
Не могут. Предположим, что d - разность такой прогрессии. Тогда при некоторых целых n,m должно быть 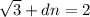 и
и 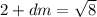 . Отсюда
. Отсюда
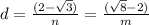 . Т.е.
. Т.е. 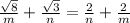 . Возводим это равенство в квадрат, и получаем, что
. Возводим это равенство в квадрат, и получаем, что 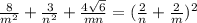 , откуда следует, что число
, откуда следует, что число 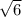 - рационально. А это не так.
- рационально. А это не так.
ПОКАЗАТЬ ОТВЕТЫ
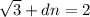 и
и 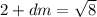 . Отсюда
. Отсюда 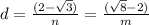 . Т.е.
. Т.е. 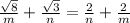 . Возводим это равенство в квадрат, и получаем, что
. Возводим это равенство в квадрат, и получаем, что 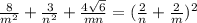 , откуда следует, что число
, откуда следует, что число 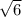 - рационально. А это не так.
- рационально. А это не так.
Другие вопросы по теме Математика
Популярные вопросы
- Что такое диффузия? эссе нужно. умоляю 8 класс. 10 предложений...
3 - Какие чудеса происходили до смерти сергия радонежского ?...
1 - Что выжить неандертальцу в палеолите ?...
1 - Решите: 3 5/8-2 3/4+1/4,решите: 11/18-7/12×1/2,решите: 2 1/3× 1 5/28+2...
1 - Используя умножения,раскройте скобки 2/3(х+6; 0,4(х+2); 4(х-3/4); 1,8(х-5);...
2 - Какая книга в моем случаи прлизведение оказало на вас наибольшее воздействие....
3 - Запиши стихотворение в конце предложения поставить знаки препинания ли...
3 - Прямоугольным треугольнике авс перпендикуляр сн,опушенный из вершины прямого...
1 - Объясните смысл загаловка знание-сила ....
3 - Придумать: слодение и вычитание обыкновенных дробей...
3