1. Математика
  2. мне. Мне нужно подробно!

мне. Мне нужно подробно! ​


мне. Мне нужно подробно! ​

mileven353 mileven353    3   03.08.2020 23:16    0

Ответы
верника3 верника3  15.10.2020 15:40

324

Пошаговое объяснение:

Выберем некоторую точку функции y. Её координаты равны (x, 4x(6-x)²). Если спроецировать её на оси Ox, Oy, то мы попадём в другие вершины прямоугольника. То есть прямоугольник имеет стороны x, 4x(6-x)². Значит, площадь этого прямоугольника равна произведению сторон: S = 4x²(6-x)².

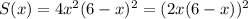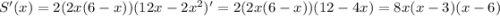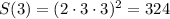Исследуем функцию площади прямоугольника S(x)=4x^2(6-x)^2=(2x(6-x))^2. Её производная S'(x)=2(2x(6-x))(12x-2x^2)'=2(2x(6-x))(12-4x)=8x(x-3)(x-6). Точки экстремума — 0, 3, 6. В промежуток (0; 6) входит только точка 3. Если 0 < x < 3, S'(x) > 0, если 3 < x < 6, S'(x) < 0. Значит, x = 3 — точка максимума. Максимальная площадь прямоугольника равна S(3)=(2\cdot 3\cdot 3)^2=324.


мне. Мне нужно подробно! ​
ПОКАЗАТЬ ОТВЕТЫ
hoseokjkjk hoseokjkjk  15.10.2020 15:40
Кому то может показаться, что излишне подробно, но это серьёзный пласт задач, хотел показать план работы
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
СоняЗагребова5 СоняЗагребова5  18.05.2021 08:37
Во 2 и 3 задачах должны быть условие, решение, ответ....
Владислава3188125 Владислава3188125  18.05.2021 08:37
Математика 6 класс все отда ​...
Ionutamaria90 Ionutamaria90  18.05.2021 08:37
Составьте систему уравнений к задаче: За 3 кг черешни и 4 кг сливы заплатили 7700 тенге. у меня СОЧ ​...
mashuljka33 mashuljka33  18.05.2021 08:37
Дополнить предложения  1.Гранью прямоугольного параллелепипеда является … 2.Равных граней у куба …. .3.Вершин у прямоугольного параллелепипеда … . 4.Ребер у прямоугольного...
nikTNG nikTNG  18.05.2021 08:38
Комбайнер в течении пяти дней убирал урожай с площадей в 18 га, 20 га, 12 га, 20 га, 15 га. 15,2 га, 16,2 га, 18,6 га, 16,2 га, 17,3 га. А) Найдите среднюю величину площади,...
данна16 данна16  18.05.2021 08:38
Решите систему уравнения и найдите значение выражения: 2xy+4y=? 4(х - у) + 2 = 5х – 3y + 23(x - 2y + 1) = 3.x - 4y + 546-6-50​...
mr1cherry mr1cherry  18.05.2021 08:39
ОООЧЕНЬ НУЖНО. СДЕЛАЙТЕ ПОЛНОЕ РЕШЕНИЕ...
nooooovikovaaaaa345 nooooovikovaaaaa345  18.05.2021 08:40
Найдите: скалярное произведение векторов...
zalomnovavk zalomnovavk  18.05.2021 08:40
В кафе Пицца в течение 15 дней фиксировалось количество заказов с доставкой на дом. Получили такой ряд данных: 39, 33,45,25,33,40,47,38,34,33,40,44,45,32,27 ​ Найдите размах...
Egorka200308 Egorka200308  18.05.2021 08:41
ОЧЕНЬ У МЕНЯ СОЧ !постройте на одной координатной плоскости графики уравнений y=2x+1 и y=3x+4 найдите координаты точек пересечения графиков и координаты пересечения с осями...

Популярные вопросы