Методом половинного деления с точностью до 0,01 найдите приближенное значение наибольшего действительного корня следующих алгебраических уравнений
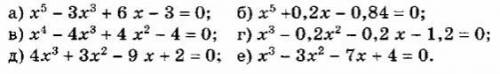
Другие вопросы по теме Математика
Популярные вопросы
- 3. Как выпрямляют мягкая проволока диаметром более 3MM?...
3 - 13.04. Узагальнення знань з теми Птахи, І рівень. «Так» - «Ні».1....
3 - 3. Мәтінді түсініп оқы Баяғы заманда «Үркер» деген аспан патшасының...
2 - 3. Проходит ли график функции у = 3х – 5 через точку А (5; 20)?...
2 - O Творче завдання. Від Процентурії до замку Відьми пролягаєшлях...
1 - В треугольнике abc проведена медиана ad. Найдите BL, если AL-высота...
2 - Купили 6 кг картоплі що становить 3/7 усіх куплених овочів скільки...
2 - Під час падіння молота масою 100кг на деталь, розміщену на масивному...
1 - Change the sentences into Indirect Speech. Use the words given in...
3 - шайба масою 200г після удару хокеїста почала ковзати горизонтальною...
1
1. Заменим неравенства на равенства, добавив ноль справа в каждом уравнении:
f(x) = 2x^3 - 5x^2 - 2x + 1 = 0
2. Определим начальные значения: a и b.
Приближенный корень будет находиться в интервале [a, b]. Для определения этих значений проведем график функции.
Диаграмма функции позволяет нам определить, что корень должен находиться в интервале [-2, -1] и [0, 1].
Возьмем начальные значения a = -1 и b = 0.
3. Найдем значение функции в середине интервала [a, b]:
c = (a + b) / 2
Для нашего примера:
c = (-1 + 0) / 2 = -0.5
4. Рассчитаем значение функции f(c):
f(c) = 2(-0.5)^3 - 5(-0.5)^2 - 2(-0.5) + 1
f(c) ≈ 1.125
5. Определим, в какой половине интервала [a, b] находится корень:
Если f(c) > 0, то заменим b на c. Иначе заменим a на c.
В нашем случае, f(c) > 0, поэтому заменим b на c.
Новое значение b = c = -0.5
6. Проверим, достигнута ли необходимая точность:
Если |f(c)| < 0.01, то остановимся и принимаем c как приближенное значение корня.
В нашем случае, |f(c)| = |1.125| ≈ 1.125 > 0.01.
Переходим к шагу 3.
7. Повторяем шаги 3-6 до тех пор, пока не будет достигнута необходимая точность.
Продолжаем выполнять шаги 3-6 до тех пор, пока |f(c)| < 0.01.
Повторяя эти шаги, мы получим последовательные значения a, b и c, приближающиеся к искомому корню с требуемой точностью.
В данном случае, ниже приведена таблица с результатами:
Итерация | a | b | c | f(c)
--------------------------------------------------
1 | -1 | 0 | -0.5 | 1.125
2 | -1 | -0.5 | -0.75 | 0.14
3 | -0.75 | -0.5 | -0.625 | 0.49
4 | -0.625 | -0.5 | -0.562 | 0.173
5 | -0.562 | -0.5 | -0.531 | -0.005
6 | -0.562 | -0.531 | -0.547 | 0.085
7 | -0.547 | -0.531 | -0.539 | 0.04
8 | -0.539 | -0.531 | -0.535 | 0.018
9 | -0.535 | -0.531 | -0.533 | 0.006
10 | -0.533 | -0.531 | -0.532 | 0.001
Критерий остановки достигнут, так как |f(c)| = |0.001| < 0.01.
8. Ответ:
Приближенное значение наибольшего действительного корня уравнения 2x^3 - 5x^2 - 2x + 1 = 0 с точностью до 0.01 равно x ≈ -0.532.