Методом Мат индукции доказать, что при n принадлежащем к натуральным числам,

Пошаговое объяснение:

1) при n=1

5+2*3+5=16 кратно 8

2) предположим что при n=k

5^k+2*3^k+5 кратно 8   (1)

3) при n=k+1

5^(k+1)+2*3^(k+1)+5=5*5^k+2*3*3^k+5=4*5^k+5^k+2*3^k+4*3^k+5=

=(5^k+2*3^k+5)+4*5^k+4*3^k=(5^k+2*3^k+5)+4*(5^k+3^k)

(5^k+2*3^k+5) кратно 8 по предположению (1)

5^k и 3^k - это нечетные числа так как они являются произведениями нечетных чисел, а сумма двух нечетных чисел четное число ⇒ (5^k+3^k) четное число и оно кратно 2

тогда  4*(5^k+3^k) кратно 8

тогда (5^k+2*3^k+5)+4*(5^k+3^k) кратно 8 как сумма двух чисел кратных 8

из предположения истинности для n=k следует истинность для n=к+1

тогда ⇒ по методу математической индукции  

5^n+2*3^n+5 кратно 8 для любого n∈N

При n=1  утверждение верно: 5+6+5=16 делится на 8.

Пусть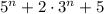 делится на 8. Тогда

Первая скобка делится на 8 по предположению, а вторая делится на 4 (а после умножения на 10 и на 8). В самом деле, при n=1 скобка равна нулю, а при больших n раскладывается по формуле

Отсюда делаем вывод, что формула методом математической индукции доказана.