Методом Эйлера найти численное решение уравнения

Другие вопросы по теме Математика
Популярные вопросы
- Назвiть за номенклатурою lUPAC алкани...
2 - Объясните смысл «Человек без людей-что тело без души....
1 - Әскери іспен айналысатын феодалдар...
2 - Скорость лодки по течению реки 15 км/ч. Найдите скорость лодки против...
1 - Почему дума Рылеева и исторические близки как жанр...
2 - 9. Вычислите: (2 - 3) (7 +43) - 43 в...
3 - Общество. нужно провести мини исследование, по предметам и по окружающего...
3 - Графически изображены скорости двух тел. Определите пути, пройденные...
3 - Закономірності поширення сейсмічних і вулканічних явищ...
3 - Почему цеха были не заинтересованы в развитии технологий (механизации...
2
Начальная точка дана по условию:
Запишем искомые решения, для нахождения х используем заданное значение шага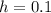 :
:
Вычислять неизвестные значения у будем по формуле:
В качестве начального значения используем координаты начальной точки:
Получим:
Таким образом, численные решения: