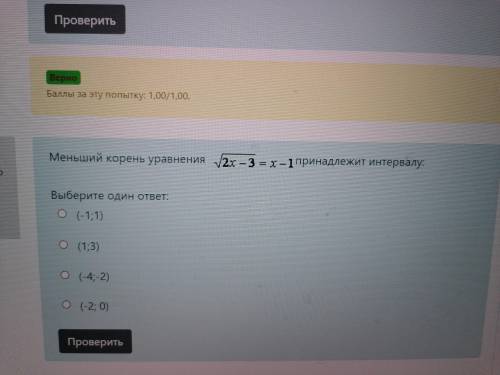
Меньший корень уравнения принадлежит интервалу

Для того чтобы найти меньший корень данного уравнения, мы должны решить его и определить интервал, в котором находится этот корень.

Первым шагом в решении данного уравнения будет выделение квадратного трехчлена через дискриминант. В данном уравнении, мы имеем a=1, b=3 и c=-2. Дискриминант выражается как D=b^2-4ac.

D = 3^2 - 4(1)(-2) = 9 + 8 = 17

Значение дискриминанта равно 17. Так как дискриминант больше нуля (D>0), это означает, что у нас есть два вещественных корня.

Далее, мы должны найти сами корни уравнения путем использования формулы корней. Формула для наших корней будет записана как x = (-b ± √D) / (2a).

Меньший корень будет соответствовать отрицательной части в формуле корня. Подставим значения a=1, b=3, c=-2 и D=17 в формулу:

x = (-3 - √17) / (2*1)

x = (-3 - √17) / 2

Таким образом, мы получили меньший корень нашего уравнения.

Чтобы определить интервал, в котором находится меньший корень, мы можем построить ось чисел и изобразить на ней линию, соответствующую значению меньшего корня.

Для этого мы можем вычислить приближенное значение корня, заменяя значение √17 на его десятичное приближение:

x ≈ (-3 - √17) / 2 ≈ (-3 - 4.123) / 2 ≈ (-7.123) / 2 ≈ -3.5615

Таким образом, меньший корень уравнения принадлежит интервалу (-∞, -3.5615).

В результате, ответ на данный вопрос будет следующим:

Меньший корень уравнения принадлежит интервалу (-∞, -3.5615).