1. Математика
  2. Математика. Задача по

Математика. Задача по геометрии. Сложная не могу сделать. Буду рад очень если кто то Задача на фотографии, так же известно что, bсм=20см, и h(a)см=16см


Математика. Задача по геометрии. Сложная не могу сделать. Буду рад очень если кто то Задача на фотог

aktobe1 aktobe1    2   02.11.2020 13:41    4

Ответы
COFFI228 COFFI228  02.12.2020 13:42

Пошаговое объяснение:

Т.к. пирамида правильная, следует угол между апофемой и основанием равен 90°. По теореме Пифагора находим половину длины ребра при основании, а потом и саму длину ребра основания.

\frac{a}{2}= \sqrt{b^{2}-h_{a}^{2}}=\sqrt{20^{2}-16^{2}}=\sqrt{400-256}=\sqrt{144} =12см

a=12*2=24см

Находим площадь боковой поверхности:

S_{bok}=\frac{1}{2}a\sqrt{b^{2}-\frac{a^{2}}{4} }=\frac{1}{2}*24\sqrt{20^{2}-\frac{24^{2}}{4} } =12\sqrt{400-\frac{576}{4} }=12\sqrt{400-144 }=12\sqrt{256} =12*16=192

Через косинус можно найти β

cosβ=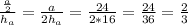\frac{\frac{a}{2} }{h_{a}}=\frac{a}{2h_{a}}=\frac{24}{2*16} =\frac{24}{36} =\frac{2}{3}

По таблицам косинусов находим угол β.

β≈48°

Диагональ основания пирамиды будет равна

d=\sqrt{2} a=24\sqrt{2}

Находим половину диагонали основания пирамиды

\frac{24\sqrt{2} }{2}=12\sqrt{2}\frac{12\sqrt{2} }{20}=0.6\sqrt{2}

По теореме Пифагора находим высоту пирамиды H:

H=\sqrt{b^{2}-(\frac{d}{2} )^{2}}=\sqrt{400-288} =\sqrt{112}=4\sqrt{7}см

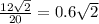
cosα=\frac{12\sqrt{2} }{20} =0.6\sqrt{2}

α≈32°

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
NUrka177 NUrka177  15.05.2020 10:28
2. Даны разложения чисел на множители. Найди их НОК и НОД: 1) а = 2∙2∙3∙5∙7, b = 2∙5∙5∙5∙7; 2) а = 3∙7∙13; b = 2∙3∙3∙17; с = 2∙5∙5∙17....
kseniy20001 kseniy20001  15.05.2020 10:28
Выполнить математический диктант.(ответы через запятую) 1) 960 уменьшить в 80 раз. 2)Найди разность чисел: 760 и 540. 3)Найди произведение чисел: 240 и 3. 4)Делимое 510, делитель...
Eugene1223 Eugene1223  15.05.2020 10:28
вычислить. Распишите подробно как решать...
gtgcfgsg6567 gtgcfgsg6567  15.05.2020 10:28
Номер 7.Можно с условием?Если будет с условием,сделаю лучшим ответом...
Топовыйшкольник Топовыйшкольник  15.05.2020 10:28
1338.Вычислите, выразив дроби в натуральных числах...
RykaBa3yka RykaBa3yka  15.05.2020 10:28
До басейну підведено три труби. Через першу трубу вся вода витікає за 12 год, через другу басейн наповнкеться за 8 год, а череа третю за 6 год. Яка частина басейну напониться за...
bistreeee bistreeee  15.05.2020 10:28
Вычисли сумму первых 10 членов арифметической прогрессии (an), если даны первые члены: −2;0... S10 =...
миша29112000 миша29112000  15.05.2020 10:28
В зависимости от строения углеводороды проявляют химические свойства вступают в реакции разных типов. Установите соответствие между классом угледородов уравнением и типом реакции​...
easyotvet01 easyotvet01  15.05.2020 10:28
Придумать 3 задачи на проценты с сюжетом из любимой сказки. Решить задачи с пропорции....
toseshevaanna toseshevaanna  09.09.2021 16:44
Выпишите элементы этих множеств,если это возможно: A={x|-1≤x≤7,eZ}...

Популярные вопросы