Математика нужно решение и ответ
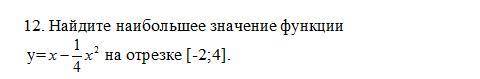
Другие вопросы по теме Математика
Популярные вопросы
- Как из 1/1000 сделать натуральное число? : с...
2 - Безударная проверяемая гласная корня содержится в ряду слов 1)...
3 - Слова похожие по звучанию(рифмы)шарик лягушка машина шоколад чай...
2 - 2предложения с описательным оборотом...
1 - Підскажіть тему для інтерв’ю з діком сендом.(п’ятнацитирічний капітан.)...
1 - Язык _сочинение- зима,самое лучшее время года...
3 - Проект 2 класс на тему что такое наука или творчество...
1 - Отношение к жизни жабы из сказки о жабе и розе...
3 - Решите две бригады работая вместе заготовили 1320 т силоса.ежедневно...
3 - Степь,рожь,глушь просклонять ,одинаковые ли окончания падежные...
3
ответ: 1.
Пошаговое объяснение:
Функция непрерывна на данном отрезке. Её производная y'=1-1/2*x при переходе через точку x=2 меняет знак с + на - , поэтому данная точка является точкой максимума функции. Так как она принадлежит отрезку [-2;4], то наибольшее значение функция имеет именно в точке x=2 и оно равно y(2)=1.
Впрочем, можно обойтись и без производной, если записать функцию в виде y=1-1/4*(x-2)². Отсюда сразу ясно, что наибольшее значение функции, равное 1, достигается при x=2.