Математика №2 1!+2!+3!+...+n! найдите сумму всех n натуральных чисел, сумма которых равна квадрату числа.
Другие вопросы по теме Математика
Популярные вопросы
- Почему гражданская война считается самой трагической страницей в истории...
1 - Где применяли труд рабов? в Риме...
3 - Как назывались и что собой представляли римские многоэтажные дома?...
2 - Почему восстания рабов терпели неудачу?...
3 - Как вы думаете, могли ли преобразования Суллы вы вести Республику...
2 - Составьте рассказы о Гнее Помпее и Марке Крассе...
2 - Какие реформы проводили Тиберий и Гай Гракхи? Что стало причиной гибели...
1 - Расскажите о реформах Цезаря. Почему считают, что он опередил свое...
2 - Что означают титулы император принцепс Август?...
1 - Почему, перейдя Рубикон, Цезарь произнес: Жребий брошен?...
2
Пусть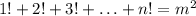 . Заметим, что при
. Заметим, что при 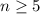 величина слева
величина слева 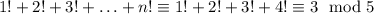 , а потому при
, а потому при 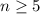 решений нет. Остается проверить
решений нет. Остается проверить 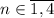 :
: 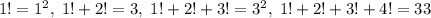 , итого =, решениями являются
, итого =, решениями являются 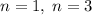 , их сумма
, их сумма 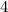 .
.