Математика ( 1 курс решить
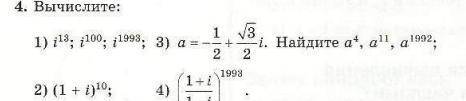
Другие вопросы по теме Математика
Популярные вопросы
- Хелп описание заповедника Завидово по плану: 1.географическое положение 2.история...
1 - Курделі сойлем курау синтаксистик талдауга с...
2 - Найдите наименьшее значение функции у=2/х - х^2 на отрезке [-2;-1/2]...
2 - Устройство общества финикии ( названия...
3 - Спишите вставляя пропущенные буквы и расставляя знаки препинания. Укажите наречия...
1 - Запишите уравнение гидролиза Бутанамида...
2 - The British are known as a nation of gardens. Most people have a garden (1) their...
3 - Какие третьи продукты можно получить в реакциях 1)Купрума, 2)Цинка, 3)Магния, 4)Натрия...
3 - Вычислите массовую долю соли в процентах, которая получится при смешивании 200 г...
2 - составить объявление на любую тему!! (6 класс)...
2
Пошаговое объяснение:
1) i ^ 13 = (i^2)^6 * i = (-1)^6 * i = i
i^100 = (i^2)^50 = (-1)^50 = 1
i^1993 = (i^100)^19 * i^93 = 1 * (i^2)^46 * i = i
2) (1 + i)^10
Воспользуемся формулой Муавра
z^n = r^n(cos φn + i*sin φn)
r - модуль, φ - аргумент комплексного числа
В нашем случае r = √2, φ =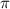 /4
/4
(1 + i)^10 = (√2)^10 * (cos 10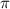 /4 + i*sin 10
/4 + i*sin 10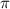 /4) = 32*(cos 5
/4) = 32*(cos 5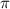 /2 + i*sin 5
/2 + i*sin 5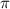 /2)=
/2)=
= 32*(0+i*1) = 32i
Другой вариант решения:
(1 + i)^10 = ( (1 + i)^2 )^5 = (1 - 2i + i^2)^5 = (1 + 2i - 1)^5 = (2i)^5 = 32i * i^4 = 32i
3) a = -1/2 + √3/2 * i
z^n = r^n(cos φn + i*sin φn)
Посчитаем модуль комплексного числа a:
r =√( (-1/2)^2 + (√3/2)^2) = 1
Аргумент φ = 2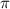 /3
/3
a^4 = 1^4 * (cos 8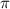 /3 + i*sin 8
/3 + i*sin 8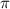 /3) = -1/2 + i*√3/2 = a
/3) = -1/2 + i*√3/2 = a
a^11 = 1^11 * (cos 22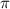 /3 + i*sin 22
/3 + i*sin 22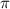 /3) = -1/2 - i*√3/2
/3) = -1/2 - i*√3/2
a^1992 = (a^4)^498 = a^498 =
= 1^498 * (cos 498*2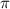 /3 + i*sin 498*2
/3 + i*sin 498*2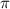 /3) = cos 332
/3) = cos 332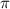 + i*sin 332
+ i*sin 332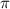 =
=
= 1
4) ( (1 + i)/(1 - i) )^1998 = ( (1 + i)^2 / 1^2 - i^2 )^1998 = ((1 + i)^2 / 2)^1998 =
= ((1^2 + 2i + i^2)/2)^1998 = ((1 +2i - 1)/2)^1998 = i^1998 = (i^2)^999 =
= (-1)^999 = -1