1. Математика
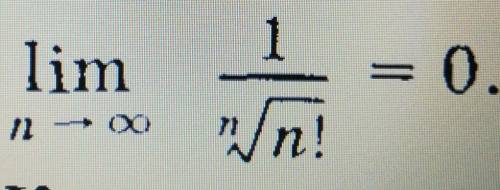
  2. Мат анализ. Доказать равенство

Мат анализ. Доказать равенство


Мат анализ. Доказать равенство

kot292 kot292    1   24.10.2020 21:28    4

Ответы
ванька68 ванька68  23.11.2020 21:29

Для начала докажем неравенство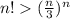 n!(\frac{n}{3})^n методом математической индукции. При n = 1 неравенство имеет место. Далее, если оно имеет место при n, то для n+1 имеем

(n+1)!n!(n+1)(\frac{n}{3})^n(n+1)=(\frac{n+1}{3})^{n+1}\cdot \frac{3}{(1+\frac{1}{n})^n}(\frac{n+1}{3})^{n+1}.

Последнее неравенство справедливо, так как

(1+\frac{1}{n})^n=1+\frac{n}{n}+\frac{n(n-1)}{2!}\cdot \frac{1}{n^2}+...+\frac{n(n-1)...(n-n+1)}{n!}\cdot \frac{1}{n^n}=\\ \\ =1+1+\frac{1}{2!}(1-\frac{1}{n})+...+\frac{1}{n!}(1-\frac{1}{n})(1-\frac{2}{n})...(1-\frac{n-1}{n})< \\ \\

Существование и равенство нулю предела вытекает из неравенства

0 справедливого \forall \varepsilon0 при всех n\frac{3}{\varepsilon}.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Nаstуа23 Nаstуа23  28.09.2019 17:30
Докажите , что числа 260 и 693 взаимно простые...
ЯтвойНос ЯтвойНос  28.09.2019 17:30
Сросно; у вовы есть 12 карточек от 1 до 12.какое наименьшее количество из этих карточек нужно взять не глядя, чтобы среди них обязательно нашлись 2 карточки с произведением чисел...
Tim4ik2281 Tim4ik2281  28.09.2019 17:30
Вчисле57493 цифра 7 обозначает количество...
valeriehunt valeriehunt  28.09.2019 17:30
31/60 : (-3,1) легко,но я что то не пойму...
Тимур00000000 Тимур00000000  28.09.2019 17:30
1. указать верно утверждение: а)любое число в отрицательной степени меньше нуля. б)любое число в нулевой степени равно нулю. в)выражение 0^n не имеет смысла 2. расставить в порядке...
nut56 nut56  28.09.2019 17:30
Решить все номера. 1)число 560 разделить на простые числа 2) какую цифру можно записать вместо звездочки в числе 329* чтобы оно делилось на 9, делилось на 5, было кратно 6? 3)...
innapuna8 innapuna8  28.09.2019 17:30
Всборнике 18 казах.народн.сказок а русс.в 2 меньше.сколько всего казахск.и русс. сказок в сборнике....
krisa2003p08dzp krisa2003p08dzp  28.09.2019 17:30
Как решить пример 123+10000000000+70000876÷76666666+5555-4253. 11-в...
apivo apivo  28.09.2019 17:30
Чо, комбиноторная . школьные туристы решили совершить путешествие к горному озеру. первый этап пути можно преодолеть на поезде или автобусе. второй этап - на байдарках, велосипедах...
ArtemkaRus71 ArtemkaRus71  28.09.2019 17:30
Если число 29450 уменьшить на 4 сотни получится...

Популярные вопросы