Люди надо молю 100 !
вершины пирамиды находятся в точках a(1,3,1), b(-1,4,6), c(-2,-3,4), d(3,4,-4).
вычислить: a)площадь грани acd; б)объем пирамиды abcd
Другие вопросы по теме Математика
Популярные вопросы
- 3. Сүйлөм түзгүлө. Көчөсүндө, тигүү, Элебапаптар, болот, филармониярында, опера...
2 - Виникнення держави.1Із запропонованого переліку причин укажіть загальні (характер-ні...
3 - Целые числа x1, x2… x21 удовлетворяют следующему уравнению: x1x2...x21=(8−x1)(8−x2)...(8−x21)....
3 - найди три последовательных натуральных числа для которых разность квадрата...
2 - Нужно найти площадь параллелограмма!...
2 - Напишите вывод об отношении Обломова к женщинам...
2 - НУЖНО КОЛ-ВО ЛЕЙКОЦИТОВ В 1 мм в кубе и форма,МЕСТО ОБРАЗОВАНИЯ,СРОК ЖИЗНИ,МЕСТО...
1 - Трудоёмкость производства сахарной свеклы ...
2 - РЕШИТЕ Это задание которое есть на фото...
3 - What sports are popular in Uzbekistan?...
2
S=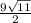 ; V=3
; V=3
Пошаговое объяснение:
Даны координаты пирамиды: A1(1,3,1), B(-1,4,6), C(-2,-3,4), D(3,4,-4)
Объем пирамиды, построенной на векторах AB(X1;Y1;Z1), AC(X2;Y2;Z2), AD(X3;Y3;Z3) равен:
здесь X,Y,Z координаты вектора.
Найдем вектора:
AB(-2;1;5)
AC(-3;-6;3)
AD(2;1;-5)
Где (-18) нашли как определитель матрицы.
∆ = -2*((-6)*(-5) - 1*3) - -3*(1*(-5) - 1*5) + 2*(1*3 - (-6)*5) = -18
Площадь грани ACD находим как половину модуля векторного произведения векторов AC и AD
AC(-3;-6;3)
AD(2;1;-5)
S=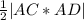
векторное произведение
AC*AD = = i ((-6)·(-5) - 3·1) - j ((-3)·(-5) - 3·2) + k ((-3)·1 - (-6)·2) = i (30 - 3) - j (15 - 6) + k (-3 + 12) = {27; -9; 9}
Модуль вектора
|AC*AD| =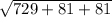 = √891 = 9√11
= √891 = 9√11
S=