1. Математика
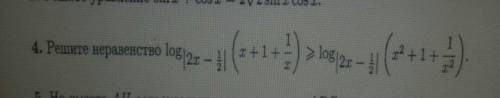
  2. Логарифмическое неравенство

Логарифмическое неравенство


Логарифмическое неравенство

муслима18 муслима18    3   02.08.2020 11:53    1

Ответы
art171 art171  15.10.2020 15:38

ОДЗ:

\left \{ {{x+1+\frac{1}{x} 0} \atop {{x^2+1+\frac{1}{x^2}0 \atop{|2x-\frac{1}{2} |\neq 0}} \right.      \left \{ {\frac{x^2+x+1}{x} 0} \atop {{ x \in R \atop{x\neq \frac{1}{4} }} \right.   ⇒  x ∈( 0 ; \frac{1}{4} ) U ( \frac{1}{4};+\infty)

Если

|2x-\frac{1}{2} |1 логарифмическая функция возрастает, большему значению функции соответствует большее значение аргумента:  

\left \{ {{|2x-\frac{1}{2} |1} \atop {x+1+\frac{1}{x} \geq x^2+1+\frac{1}{x^2} }} \right.         \left \{ {{2x-\frac{1}{2} < -1 ; 2x-\frac{1}{2} 1 } \atop {x+\frac{1}{x} \geq(x+\frac{1}{x}) ^2-2 }} \right.   ⇒ замена переменной x+\frac{1}{x} =t

D=(-1)²-4·(-2)=9;  корни  t₁=1;  t₂=2

C учетом ОДЗ:

\left \{ {{x\frac{3}{4} } \atop {(x+\frac{1}{x}-1)(x+\frac{1}{x}-2)\leq 0 }} \right.   ⇒  x^2-2x+1 ≤0  ⇒  (x-1)²≤0    ⇒   x=1  

Если

0  логарифмическая функция убывает, большему значению функции соответствует меньшее значение аргумента:  

\left \{ {{0       \left \{ {{-1  ⇒ замена переменной x+\frac{1}{x} =t

D=(-1)²-4·(-2)=9;  корни  t₁=1;  t₂=2

C учетом ОДЗ:

\left \{ {{0    ⇒  x^2-2x+1 ≥0  ⇒(x-1)²≥0  x - любое

x \in (0; \frac{1}{4})\cup (\frac{1}{4}; \frac{3}{4})

О т в е т. x \in (0; \frac{1}{4})\cup (\frac{1}{4}; \frac{3}{4})\cup{1}

ОДЗ:

\left \{ {{x+1+\frac{1}{x} 0} \atop {{x^2+1+\frac{1}{x^2}0 \atop{|2x-\frac{1}{2} |\neq 0}} \right.      \left \{ {\frac{x^2+x+1}{x} 0} \atop {{ x \in R \atop{x\neq \frac{1}{4} }} \right.   ⇒  x ∈( 0 ; \frac{1}{4} ) U ( \frac{1}{4};+\infty)

Применяем метод рационализации логарифмических неравенств:

(|2x-\frac{1}{2}|-1)\cdot (x+1+\frac{1}{x}- x^2-1-\frac{1}{x})\geq 0

(|2x-\frac{1}{2}|-1)\cdot( (x+\frac{1}{x})^2-(x+\frac{1}{x})- 2)\leq 0

Решаем неравенство методом интервалов:

1)

|2x-\frac{1}{2}|-1= 0     ⇒      |2x-\frac{1}{2}|=1   ⇒

2x-\frac{1}{2}=-1          или               2x-\frac{1}{2}=1

x=-\frac{1}{4}   не входит в ОДЗ       или       x=\frac{3}{4}

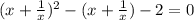
2)(x+\frac{1}{x})^2-(x+\frac{1}{x})- 2=0

Замена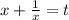   x+\frac{1}{x}=t

t^2-t-2=0

t_{1}=1   или    t_{2}=2

x+\frac{1}{x}=1    или   x+\frac{1}{x}=2

\frac{x^2-x+1}{x}=0    или   \frac{x^2-2x+1}{x}=0

нет корней    или    x=1

Расставляем знаки неравенства

(|2x-\frac{1}{2}|-1)\cdot( (x+\frac{1}{x})^2-(x+\frac{1}{x})- 2)\leq 0

на ОДЗ:

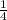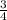(0) _-___ ( \frac{1}{4} ) _____-____ ( \frac{3}{4} ) ____+_____  [1} ___+___

О т в е т.x \in (0; \frac{1}{4})\cup (\frac{1}{4}; \frac{3}{4})\cup{1}

ПОКАЗАТЬ ОТВЕТЫ
зуляжансая86 зуляжансая86  15.10.2020 15:38

ответ:(0;1/4)∪(1/4;3/4)∪{1}

Пошаговое объяснение: см. во вложении

Добавлю еще первое неравенство, которое решал методом интервалов. дла случая а)2*(х-3/4)*(-(х-1)²/х)*((х²+1-х)/х)≥0

Для случая б) -2*(х+1/4)*(-(х-1)²/х)*((х²+1-х)/х)≥0


Логарифмическое неравенство
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
termos68 termos68  17.09.2020 01:55
люди получил от учителя Пусть х - количество кустов смородины, тогда количество кустов крыжовника равно (х+3),а количество кустов малины 2 (х+3).По условию задачи, в саду...
kmelnuk5 kmelnuk5  17.09.2020 01:55
Впр не могу решить( надеюсь кто нибудь...
Boba35 Boba35  17.09.2020 03:30
Кез-келген үшбұрыштың ішкі рыштарының қосындыс 8. Бірінші санның екінші санға қатынасы 3:5, ал екінші санның үшінші санга қатынасы 7:11. Бірінші санның үшінші санға қатынасын...
QueenKulumshina QueenKulumshina  17.09.2020 03:31
8. ДА 149. 1) Көлемі 180 дм3 және ені 15 дм болатын тікбұрышты паралле- лепипедтің ұзындығы мен биіктігі; 2) 650 теңгеге сатып алынған матаның ұзындығы мен 1 м ма- таның...
Tanya11011 Tanya11011  17.09.2020 05:47
Я буду вам очень благодарна...
09Катя99 09Катя99  17.09.2020 04:56
Помагите ришить задачу ребята повели лошадей на водопой. Сколько было ребят и сколько лошадей варианты ответов:1вариант 13ребят и 13лошадей, 2вариант: 11ребят и 15лошадей.3...
znikitai znikitai  17.09.2020 04:50
и 6 ❤❤ ни понимаю ни как ​...
юля2713 юля2713  17.09.2020 04:45
Бөлменін көлемі v м 3 биіктігі 3 см , бөлменің еденінін ауданын тап мұндағы v ,- 120 ​...
BlackGus007 BlackGus007  17.09.2020 04:45
хелп щч впр нужно капец быстрее спс за ранее...
Аннабель0Свит Аннабель0Свит  17.09.2020 01:55
Решите очень надо Я ХОЧУ 3!!1 (4+2j)^3 либо это (1+2j)X+(3-5j)y=1-3j тема комплексные числа...

Популярные вопросы