Логарифмические уравнения. Решите
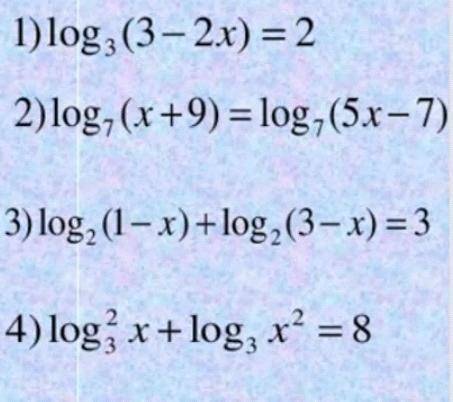
Другие вопросы по теме Математика
Популярные вопросы
- 1. Какова расстояние между шарами массой 100 кг каждая, которые находятся в...
1 - 4. Спишите, вставляя пропущенные буквы и раскрывая скобки. Расставьте пропущенные...
2 - Твір За яким ліідером пішов би я ...
1 - Выбери, какие из суждений верны. А. Аскарида относится к Типу Ресничные черви....
2 - Прочитай, как Марк с Алисой провели воскресный день Раскрой скобки, поставь...
2 - Автомобиль массой 1т движется под гору при включенном моторе с постоянной скоростью...
3 - Вопросы по теме бактерии парази́ты́ рифмованные...
3 - В пчелином языке 4 различных движений головой и 11 брюшком причём движения...
1 - утворіть словотворні ланцюжки від таких слів: друг,дощ, співати визначте твірні...
2 - Что сделал Лотарь? очень нужно ...
3
Пошли нафиг л*х л*х л*х
1. Изначально мы имеем следующее уравнение: log2(x + 1) + log2(3 - x) = 2.
2. Для упрощения уравнения мы можем использовать свойство логарифма, согласно которому сумма логарифмов с одинаковым основанием эквивалентна логарифму произведения этих чисел.
Таким образом, мы можем записать уравнение в следующем виде: log2((x + 1) * (3 - x)) = 2.
3. Теперь мы можем применить обратное свойство логарифма, которое гласит, что логарифм числа по определенному основанию равен степени этого основания, возводимой в полученное число.
Таким образом, мы можем записать уравнение в следующем виде: (x + 1) * (3 - x) = 2^2.
4. Избавимся от скобок, перемножив элементы внутри них: x^2 - x + 3 - x = 4.
Это уравнение можно упростить до x^2 - 2x - 1 = 0.
5. Теперь мы можем решить полученное квадратное уравнение. Мы можем использовать квадратное уравнение, с помощью которого найдем значения x.
Решение данного квадратного уравнения представляется формулой: x = (-b ± sqrt(b^2 - 4ac)) / (2a).
В нашем случае a = 1, b = -2 и c = -1.
Подставим их в формулу:
x = (-(-2) ± sqrt((-2)^2 - 4 * 1 * (-1))) / (2 * 1).
Продолжим вычисления:
x = (2 ± sqrt(4 + 4)) / 2.
x = (2 ± sqrt(8)) / 2.
x = (2 ± 2sqrt(2)) / 2.
6. Теперь мы можем упростить это выражение, разделив числитель и знаменатель на 2:
x = 1 ± sqrt(2).
Таким образом, получаем два действительных значения: x = 1 + sqrt(2) и x = 1 - sqrt(2).
Таким образом, решением данного логарифмического уравнения являются два значения: x = 1 + sqrt(2) и x = 1 - sqrt(2).
Я надеюсь, что эта подробная пошаговая информация помогла вам понять процесс решения данного уравнения. Если у вас возникнут еще вопросы, пожалуйста, не стесняйтесь спрашивать.