Log7 (x - 1) log7 x = log7 x;
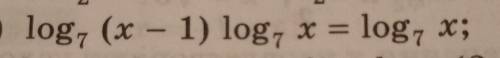
Другие вопросы по теме Математика
Популярные вопросы
- скорее Mark the proper form of the verb:a story about a wolf...
2 - нужно Уравнение координаты материальной точки имеет вид: = 48...
2 - 1. Определите обеспеченность разными видами ресурсов выбранной...
1 - K2 [cu (cn) 4] уравнения диссоциации первичной и вторичной (обязательно...
2 - 1) Найти область определен ия функции: а) y= 2) y= 2)Постройте...
2 - Предложите 3 пункта значения растенийпредложите 3 пункта значения...
3 - Выполните перевод с этой заданией умоляю вас...
2 - 2 Выберите прилое ранеесте! B) 55555-5-17355-53-357D) 3555-55-3573....
2 - Делаю испанский, какое последнее слово?✌...
2 - Напишите описания любой из ,Картины с выставки ‘’...
3
У нас есть уравнение:
Log7 (x - 1) log7 x = log7 x
Посмотрим на каждую часть выражения по отдельности.
1. Log7 (x - 1): это логарифм числа (x - 1) по основанию 7. Логарифм - это функция, которая показывает, в какую степень нужно возвести заданное число (основание) для получения другого числа (аргумент). В данном случае, мы ищем такую степень, чтобы 7 возводилось в нее и равнялось (x - 1).
2. log7 x: это логарифм числа x по основанию 7. Мы также ищем такую степень, чтобы 7 возводилось в нее и равнялось x.
Теперь давайте займемся упрощением данного уравнения.
У нас есть два логарифма, которые равны между собой. Чтобы решить это уравнение, мы можем равенство логарифмов переписать в виде экспоненты, используя свойство логарифмов.
Свойство: loga b = c эквивалентно a^c = b.
Применяя это свойство к нашему уравнению, получим:
(7^(log7 (x - 1)))^(log7 x) = 7^(log7 x)
Здесь мы применили свойство логарифма, чтобы избавиться от логарифма и превратить его в экспоненту с результатом 7^c.
Теперь, как известно, (a^b)^c = a^(b*c), так что мы можем упростить наше уравнение:
7^((log7 (x - 1))*(log7 x)) = 7^(log7 x)
Мы получили равенство двух экспонент.
Теперь, чтобы уравнение было верным, показатели степеней в обеих частях должны быть равны.
Таким образом, у нас есть:
(log7 (x - 1))*(log7 x) = log7 x
Теперь мы можем избавиться от логарифма и решить это уравнение.
Мы можем сократить обе стороны на log7 x, потому что log7 x / log7 x = 1.
Таким образом, у нас остается:
log7 (x - 1) = 1
Теперь мы можем переписать это уравнение в экспоненциальной форме, используя определение логарифма.
Из определения логарифма: loga b = c эквивалентно a^c = b.
Таким образом, мы имеем:
7^1 = x - 1
Так как 7 возводится в степень 1 и равно 7, у нас получается:
7 = x - 1
Теперь, чтобы решить это уравнение и найти значение x, нужно избавиться от -1.
Мы можем добавить к обеим сторонам уравнения 1:
7 + 1 = x - 1 + 1
8 = x
Итак, мы получаем, что значение x равно 8.
Ответ: x = 8.