1. Математика
  2. Log5(x-3)+2=log5(x-2)+log3(

Log5(x-3)+2=log5(x-2)+log3( 5)

talyaarpaci talyaarpaci    2   29.10.2020 17:00    0

Ответы
KÆTÉ KÆTÉ  28.11.2020 17:00

x=\dfrac{2\cdot5^{\log_35}+75}{25+5^{\log_35}}

Пошаговое объяснение:

1 Запишем уравнение

\log_5(3-x)+2=\log_5(x-2)+\log_35\\

2 Запишем ОДЗ: аргумент логарифма строго больше 0

\displaystyle \left \{ {{3-x0} \atop {x-20}} \right.

3 Решим эту систему неравенств

\displaystyle \left \{ {{3-x0} \atop {x-20}} \right.\Leftrightarrow \left \{ {{3x} \atop {x2}} \right.\Leftrightarrow x\in(2;3)

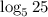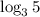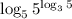
4 Запишем 2 как \log_525 и \log_35 как \log_55^{\log_35}

\log_5(3-x)+\log_525=\log_5(x-2)+\log_55^{\log_35}

5 Воспользуемся формулой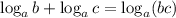 \log_ab+\log_ac=\log_a(bc)

\log_5\bigg((3-x)\cdot25\bigg)=\log_5\bigg((x-2)\cdot5^{\log_35}\bigg)

6 Уберем логарифмы (все ограничения записаны в ОДЗ)

(3-x)\cdot25=(x-2)\cdot5^{\log_35}

7 Перед нами линейное уравнение

75-25x=5^{\log_35}x-2\cdot5^{\log_35}

8 Все что с х налево, все что без направо

-25x-5^{\log_35}x=-2\cdot5^{\log_35}-75

9 Умножим все на -1 и вынесем х

\big(25+5^{\log_35}\big)x=2\cdot5^{\log_35}+75

10 Выразим х

x=\dfrac{2\cdot5^{\log_35}+75}{25+5^{\log_35}}

11 Оценим значение, чтобы понять, принадлежит ли оно промежутку

\dfrac{2\cdot5^{\log_35}+75}{25+5^{\log_35}}\approx\dfrac{2*10.6+75}{25+10.6}\approx\dfrac{96.13}{35.57}\approx2.703

Принадлежит промежутку.

Тогда это ответ!

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
МЯУСИМ2007 МЯУСИМ2007  11.04.2019 12:25
Составьте множество двузнчных чисел a, b, c, в записи которых использется лишь цифры: 1) 2 и 6; 2; )0, 1 и 7; 3)3, 5 и 9; ​...
124541Artem11111 124541Artem11111  11.04.2019 12:25
Для зависимой переменной y найдите его значение при заданных x равной 5; - 2; 1,3; -0,8. если[tex]y = 3x + 1[/tex] ​...
sonykit2006 sonykit2006  11.04.2019 12:24
Функции f(x)=3x^2 -2 найдите первообразную график который проходит через точку m (2; 5)...
Phelper Phelper  11.04.2019 12:21
Впервом контейнере находится 2 коробок с посудой и 5 ко- робок с книгами, а во втором контейнере — 3 коробок с посудой и 6 коробок с книгами. из первого контейнера во второй переложили...
likeaboss2005 likeaboss2005  11.04.2019 12:21
Знайдіть довжину кола, радіус якого дорівнює 10 см​...
negatiff95 negatiff95  11.04.2019 12:20
Кто-нибудь мне объяснит почему в 3 номере, -9х+4х получилось -13х. это в глаз решили не правильно ?...
kostyaluch kostyaluch  11.04.2019 12:20
Водин магазин 24 мешка картофеля а в другой 28 мещков. во магазин на 160кг больше, чем в первый. сколько килограммов картофеля в каждый магазин...
btrawee34 btrawee34  11.04.2019 12:19
Мирозвиль 9 лет его возраст составляет 25 возраста отца,а возраст отца 60 возраста дедушки сколько лет дедушке мираса​...
ichmaelz ichmaelz  11.04.2019 12:19
Найдите a) s10,если d= -4 , a10=-20; b)n,если а1= -8; d=0,5 и аn= -3​...
Юлия111157 Юлия111157  11.04.2019 12:18
Сравни выражения не вычисляя х х-с какой поставить знак больше,меньше или равно...

Популярные вопросы