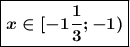Log3(x^2+2)- log 3 (x^2-x+12) > = log3(1+ 1/x)
Другие вопросы по теме Математика
Популярные вопросы
- Вмагазин 106 л масла в 5-литровых и 7-литровых банках.сколько 5-литровых и 7-литровых...
2 - Расшифруйте слово переставив в нем буквы в правильном порядке дйрутны какое слово...
3 - Какие возможности нам даёт .язык сочинение...
2 - Выпиши все существительные они обязательны для всех стран и народов они это существительное...
1 - Какие из них глаголы неопределённой формы пишут,говорил,наказывать, смотреть,появляется,...
3 - Длина поле 130м, ширина 70м 1/5 участка засеяно картофелем. сколько квадратных метров...
3 - Расстояние между землей и луной равно 365 400 км.за сколько времени движующееся...
3 - Написать эссе на тему цена победы великой отечественной войны ....
2 - Умей дерево что тут надо вставить?...
1 - Сдвух аэродромов, расстояние между которыми 1495 км. вылетели навстречу друг другу...
1
ОДЗ : 1) x²+2>0 ⇒ x∈R
2) x²-x+12>0 ⇒ D=1-4·12=-47<0 ⇒ x∈R
3)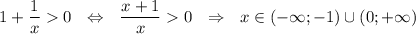
ОДЗ : x ∈ (-∞; -1) ∪ (0; +∞)
x² - x + 12 > 0 всегда, так как D < 0 ⇒
Метод интервалов : x₁ =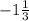 ; x₂ = 0
; x₂ = 0
+++++++++++![[-1\frac{1}{3}]](/tpl/images/0919/4650/98da6.png) ----------- (0) +++++++++++> x
----------- (0) +++++++++++> x
С учётом ОДЗ :