1. Математика
  2. Log0.6(3-2x) log0.6(5x-2)

Log0.6(3-2x)>log0.6(5x-2)

Malika274 Malika274    2   31.12.2020 11:21    0

Ответы
1232890 1232890  31.12.2020 11:30

(\frac{5}{7} ; ^{ } \frac{3}{2} )

Пошаговое объяснение:

ОДЗ:

\left \{ {{3-2x0} \atop {5x-20}} \right. ;\\\left \{ {{x\frac{2}{5} }} \right.

log0.6(3-2x)log0.6(5x-2)\\3-2x5\\x\frac{5}{7}

ПОКАЗАТЬ ОТВЕТЫ
Jihye11 Jihye11  31.12.2020 11:30

log_{0.6}(3-2x)log_{0.6}(5x-2)

ОДЗ:

Подлогарифменное выражение должно быть всегда больше нуля. Найдём значения x, при которых выражение 3-2xотрицательно или равно нулю:

3-2x\leq0\\\\\\-2x\leq3\\\\\\x\geq\dfrac{3}{2}

Аналогично с 5x-2:

5x-2\leq0\\\\\\5x\leq2\\\\\\x\leq\dfrac{2}{5}

Отсюда:

x\in\Big(\dfrac{2}{5};\dfrac{3}{2}\Big)

=========================

Так как основания логарифмов равны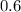 0.6, то логарифмы можно убрать, но поменять знак неравенства на противоположный:

3-2x

Решаем получившееся неравенство:

-2x-5x

Находим пересечение с ОДЗ:

x\in\Big(\dfrac{5}{7};+\infty\Big)\cap\Big(\dfrac{2}{5};\dfrac{3}{2}\Big)\\\\\\x\in\Big(\dfrac{5}{7};\dfrac{3}{2}\Big)

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
zver35 zver35  14.05.2019 19:47
Вычислите площадь равнобедренного треугольника, если его основание равно 6 см и угол при вершине равен 120°...
Alinahe2001 Alinahe2001  14.05.2019 19:47
Все нужно разписать 1 представте в виде степени с основанием n выражение : (n в степени -3) в степени 4: n в степени -15 2 выражение: √16b-0,5√36b надеюсь на вашу...
1TeD 1TeD  14.05.2019 19:46
Вокружности с центром в точке о к хорде ab,равной радиусу окружности,перпендикулярно проведён диаметр cd.диаметр cd и хорда ab пересекаются в точке k. длина отрезка ak...
egorsnaiper201 egorsnaiper201  14.05.2019 19:46
Найди площади закрашенных частей​...
RealBohdan RealBohdan  14.05.2019 19:45
Малина містить у середньому 5% цукру.скільки кілограмів цукру міститься в 30кг малини?...
Anyakeklol1314 Anyakeklol1314  14.05.2019 19:43
К200 г раствора, содержащего 4% соли, добавили воды, увеличив массу раствора на 25%. найдите процентное содержание соли в получившемся растворе....
Snoowker Snoowker  14.05.2019 19:42
Найдите произведение целых чисел расположенных между числами -12 и 120...
УмнаяДебилка УмнаяДебилка  14.05.2019 19:42
Какие цифры можно написать вместо знака ? в неравенстве, чтобы оно было верным: ​​​​ 9238 92 ? 8...
AgafAl AgafAl  14.05.2019 19:42
Зробіть будь ласка приклад (1) 10 ів...
ystefaniv ystefaniv  14.12.2020 21:29
ЗаслаDla kynnu mpanesic - 36062ова с кажут​...

Популярные вопросы