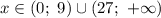Log _(3)^(2)x-5log _(3)x+6>0
очен
Другие вопросы по теме Математика
Популярные вопросы
- Прочитайте. выпишете в предложения подходящие по смыслу слова....
2 - 5міст у назв яких зустрічається імена чи прізвиська людей...
2 - Объясните своими словами , что такое натуральное хозяйство...
3 - Составить таблицу-кластер по теме природный комплекс (раздел...
1 - Найдите пару слов,которая совпадает по значению: гарантийный-гарантированный;...
1 - Что, кроме религиозного чувства, подвигло в путь феодалов, безземельных...
3 - к ужасу это вводное слово? ил уточнение? что это?...
2 - Построить график функции. y=-x^2-6x-5 y=x^2+4x+3...
3 - Дубровский стал учителем французского языка в доме троекурова...
3 - Укажите наибольшее число , двоичная запись которого содержит...
2
Введем замену: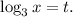
Тогда получаем соответствующее неравенство:
Обратная замена:
ответ: