1. Математика
  2. Лодка проплывает 9 км по

Лодка проплывает 9 км по течению реки и 1 км против течения за то же время, которое потребуется плоту, чтоб проплыть 4 км по этой речке. Найдите скорость течения, если собственная скорость лодки 8км/час​

love2121 love2121    2   29.10.2020 00:01    3

Ответы
nairisaaryan nairisaaryan  28.11.2020 00:02

Для начала разберемся. Скорость течения реки - x км/ч.

V = (8 + x) – cкорость лодки по течению реки.

V = (8-x) – скорость лодки против течения реки.

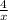4км = \frac{4}{x} часов проплывает плот.

1) лодка на путь в 9 км/ч =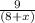 \frac{9}{(8+x)} -  по течению реки

2) против течения реки =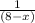 \frac{1}{(8-x)} - часов.

Переходим к решению, составляем уравнение:

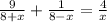
1) \frac{9}{8+x} + \frac{1}{8-x} = \frac{4}{x}

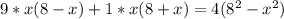
2) 9*x(8-x)+1*x(8+x)=4(8^{2} - x^{2})

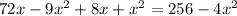
3) 72x - 9x^{2} + 8x + x^{2} = 256 -4x^{2}

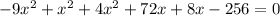
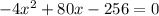
4)-9x^{2} +x^{2} + 4x^{2} +72x + 8x - 256 = 0

5) -4x^{2} + 80x - 256 = 0

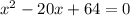
6) x^{2} - 20x + 64 = 0

Согласно теореме Виета =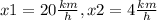 x1 = 20 \frac{km}{h} , x2 = 4 \frac{km}{h}

ответ: 4 км/ч

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Tatuhenka3 Tatuhenka3  22.05.2019 01:00
На карточках выписаны числа от 1 до 10 (на одной карточке – одно число). карточки положили на стол и перемешали. найти вероятность того, что на вытащенной карточке...
stasikpavel stasikpavel  22.05.2019 01:00
Ложка,которая стоила 30 рублей,продаётсяс10%-й скидкой.при покупке 10 таких ложек покупатель отдал кассиру 500 рублей. сколько рублей сдачи он должен получить? напишите...
папапапппаапап папапапппаапап  22.05.2019 01:00
Из коробки конфет взяли 25% всех конфет,а потом 75% оставшихся. осталось 27 конфет. сколько конфет было первоначально...
вира7 вира7  22.05.2019 01:00
Что больше: 25% от(-0,04) в 4 степени * 25 в 4 степени + (9 тринадцатых) в 10 степени * (- 13 девятых) в 10 степени или 15% от 8 в 4 степени * 16 в 2 степени / 8...
АнгелТих АнгелТих  22.05.2019 01:00
Сторона квадратного листа жести 1.2 м лист разрезали на куски прямоугольной формы с измерениями 1м и 0.2м. надо выяснить с чертежа, как получить наибольшее количество...
vikazinoveva03 vikazinoveva03  22.05.2019 01:00
Тарелка, которая стоила 80 рублей, продаётся с 10%-й скидкой. при покупке 10 таких тарелок покупатель дал кассиру 100 рублей. сколько рублей сдачи он должен получить?...
snaiperkiling snaiperkiling  22.05.2019 01:00
Придумать название команды для фотомарафона) нас три девочки) какое-нибудь безумное и цепляющее, только скорее, )...
Asig Asig  22.05.2019 01:00
Туристы были в пути 3 дня.в первый день они преодолели 36% всего расстояния,во второй 52 % оставшегося пути,а в третий-54 км.найти длину всего пути. решить)...
alena12022004 alena12022004  22.05.2019 01:00
Первая бригада построит за 54 дня, а вторая бригада за 27 дней. за сколько дней две бригады построят дом при совместной работе?...
alikjd8 alikjd8  22.05.2019 01:00
Сбукв с,d и e запишите сочетательное свойство сложения...

Популярные вопросы