Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами и специальной правой частью. найти общее решение уравнения.
y'' + 2y' + y = x^2 + 4
Другие вопросы по теме Математика
Популярные вопросы
- Напишіть невеликий твір-роздум на одну із тем:1. «Священні книги народів світу як...
1 - Верны ли утверждения 91 кратное числа 7...
3 - 1 Complete the sentences with some or any. There are some new students in your class....
3 - Строение атома 78,87,93,102 58,81,83,103...
3 - 0, 85×5 1/7+69,25÷27,7-14 3/20...
1 - 4-тапсырма Айтыс туралы Мұхтар Әуезов қандай пікір білдірді? Галым пікіріне назар...
1 - Задания: 1)Озаглавьте каждую приведённую статью закона. Статья 2 Статья 47 Статья...
2 - Назовите 3 условия, которые возникнуть государству Русь...
3 - Какие простые вещества имеют атомное строение. приведите пример...
2 - Между массами 5 кг и 500 г можно поставить знак... А. МеньшеБ. РавноВ. Никакой Г....
1
Найдем начала общее решение соответствующего однородного дифференциального уравнения
Воспользовавшись заменой Эйлера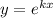 , мы получим характеристическое уравнение
, мы получим характеристическое уравнение
Общее решение уравнения (*)
Далее нужно найти частное решение. Рассмотрим функцию:
Здесь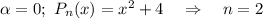
Сравнивая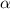 с корнями характеристического уравнения и, принимая во внимая, что
с корнями характеристического уравнения и, принимая во внимая, что 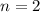 частное решение будем искать в виде
частное решение будем искать в виде
Подставляем все это в исходное дифференциальное уравнение
Приравниваем коэффициенты при степени x
Частное решение: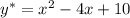
Общее решение линейного неоднородного дифференциального уравнения:
y = C1 e‾ᵡ + C2 x e‾ᵡ + x^2 -4x +10
Пошаговое объяснение:
y'' + 2y' + y = x^2 + 4
однородное уравнение имеет вид
y'' + 2y' + y = 0
составим соответствующее характеристическое уравнение
k^2 + 2k + 1 = 0
(k+1)^2 = 0
k+1 =0 > k1,2 = -1
имеем два действительных кратных корня
Общее решение однородного уравнения
yo = C1 e‾ᵡ + C2 x e‾ᵡ
Частное решение ищем в виде
yч = Ax^3 +Bx^2 +Cx +D
находим производные
yч' = (Ax^3 +Bx^2 +Cx +D)' =3Ax^2 +2Bx +C
yч" = (3Ax^2 +2Bx +C)' = 6Ax +2B
подставляем в исходное уравнение
yч'' + 2yч' + yч = 6Ax +2B + 2 (3Ax^2 +2Bx +C) + Ax^3 +Bx^2 +Cx +D =
= Ax^3 +(6A+B)x^2 + (6A+4B+C)x + (2B+2C+D) = x^2 +4
Решаем систему из соответствующих коэффициентов
x^3: A = 0
x^2: 6A+B = 1; B = 1-6A = 1-6*0 = 1
x^1: 6A+4B+C = 0; C = -6A -4B = -6*0 -4*1 = -4
x^0: 2B+2C+D = 4; D = -2B -2C = 4 -2*1 -2*(-4) =10
Частное решение имеет вид
yч = 0*x^3 + 1*x^2 -4x +10 = x^2 -4x +10
Общее решение линейного неоднородного дифференциального уравнения
y = yo + yч = C1 e‾ᵡ + C2 x e‾ᵡ + x^2 -4x +10