Lim(4/(1-x^4))-(2/(1-x^2))=бесконечность делить на - бесконечность x стремится к 1
Другие вопросы по теме Математика
Популярные вопросы
- Запишіть у вигляді десяткового дробу 2 3/10...
3 - ПОПС-формулу по теме «Нравственные мотивы поступков героя рассказа «Муму»...
3 - Дизель – электрический поезд был в пути 3 часа, двигаясь со скоростью185 км/ч....
1 - Запись романса в сопровождении гитары, определить его содержание и особенности...
2 - Перспективи розвитку атомної енергетики в україні...
3 - Назовите по 7 плюсов и минусов экономического развития России во второй половине...
2 - Из 3/5 числа 30 вычти 3/4 числа 24 . ЗАпиши полученый результат....
2 - Выпишите целые решения неравенства –14 x≤1 в порядке убывания. Только быстрее...
2 - На какие типы подразделяются манипулирующие роботизированные системы? в чем их...
2 - Фізика 9 клас фізика задача: визначте ккд атомної електростанції потужністю 1400...
3
ответ: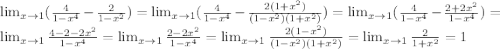
Пошаговое объяснение: