Квадратный трехчлен ax²+bx+c (a,b и c – действительные числа) имеет два различных ненулевых корня: 1 и q. после того, как никита изменил значение какого-то из коэффициентов: a, b или c, получился трехчлен, имеющий два различных корня: 2 и 3q. найдите наибольшее значение q.
Ответы
Так как корни квадратного уравнения 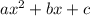 являются числа
являются числа 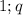 , то данный трехчлен можно представить в виде
, то данный трехчлен можно представить в виде
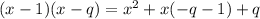 , по второму условию следует что можно представить в виде
, по второму условию следует что можно представить в виде
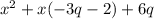 , по условию он поменял только одну переменную , очевидно что
, по условию он поменял только одну переменную , очевидно что 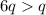 , тогда следует что только
, тогда следует что только
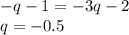
ПОКАЗАТЬ ОТВЕТЫ
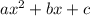 являются числа
являются числа 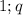 , то данный трехчлен можно представить в виде
, то данный трехчлен можно представить в виде 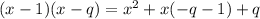 , по второму условию следует что можно представить в виде
, по второму условию следует что можно представить в виде 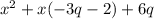 , по условию он поменял только одну переменную , очевидно что
, по условию он поменял только одну переменную , очевидно что 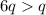 , тогда следует что только
, тогда следует что только 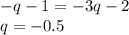
Другие вопросы по теме Математика
Популярные вопросы
- Приведите три примера наследования признаков человека по аутосомно-доминантному...
2 - Элементарный эволюционный материал — популяция. 2. Элементарная...
3 - Заполните таблицу Популяционно-статистический метод...
3 - Какие близнецы называются монозиготными?...
1 - К какому заболеванию приведет оплодотворение сперматозоидом с...
2 - В каком случае возможно рождение девочки, больной гемофилией?...
3 - Что такое конкордантность?...
2 - К какому заболеванию приведет оплодотворение сперматозоидом с...
1 - Какие признаки наследуются по аутосомно-доминантному типу:...
1 - К какому заболеванию приведет лишняя хромосома 21 пары? Укажите...
2