Кто-то Стороны треугольника равны 4 см,6 см и 9 см. Найти периметр подобного треугольника,если у подобного треугольника самая длинная сторона равна 36 см.
Заранее

Ответы

4новичок4 08.12.2020 18:30

76см

Пошаговое объяснение:

36:9=4 коэффициент подобия.

4*4=16 см первая сторона подобного треугольника

4*6=24 см вторая сторона подобного треугольника.

Периметр треугольника равен сумме всех сторон треугольника.

Р=16+24+36=76 см.

ПОКАЗАТЬ ОТВЕТЫ

aleksandrborodp06tyy 08.12.2020 18:30

Задача на подобие треугольников (коэффициенты подобия).

В первом треугольнике - стороны 4 см, 6 см и 9 см.

Во втором треугольнике - стороны X см, Y см и 36 см.

*в первом треугольнике самая большая сторона - 9 см, во втором треугольнике - 36 см (бóльшая сторона одного треугольника соотносится с большей стороной второго треугольника).

Значит они относятся с каким-то коэффициентом подобия (раз по условию треугольники подобны):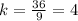 $k=\frac{36}{9} =4$ (бóльшая сторона большего треугольника разделить на бóльшую сторону меньшего треугольника).

Соответственно, теперь по этому коэффициенту можно найти оставшиеся стороны:

Первая сторона -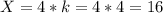 X=4*k=4*4=16 см

Вторая сторона -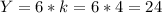 Y=6*k=6*4=24 см

Третья сторона -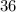 см (по условию)

Периметр большего треугольника: $P_{2} =X+Y+36=16+24+36=76$ см.

*дополнительно это можно и проверить. Периметры подобных треугольников соотносятся как коэффициент подобия:

Периметр меньшего треугольника: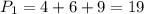 $P_{1} =4+6+9=19$ см

Тогда поделив периметр большего треугольника на меньшего треугольника мы будем должны получить этот самый коэффициент подобия (то есть 4):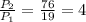 $\frac{P_{2} }{P_{1} } =\frac{76}{19} =4$ - значит задача решена верно!