Математика: Кто может объяснить как это решили (пункт а)

Рассмотрим какое-нибудь число ; Пусть 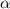- наибольшая степень десятки, которая делит ; Тогда можно представить в виде 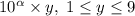; Это число имеет 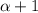цифру. Теперь 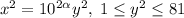; Поэтому число 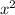имеет в своей записи не больше, чем 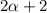цифры, но и не меньше, чем 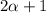цифру.Если взять первый случай, то пусть первое число ; Тогда второе число - 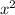, третье - 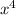; Пусть у 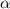цифр, а 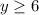; Тогда у первого числа 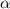цифр, у второго 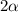, у третьего 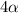. Итого 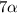цифр. Нас просят, чтоб их было 14. То есть 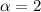. Поэтому, учитывая ограничение на 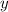, можно взять 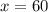; Получим ;Можно...

Кто может объяснить как это решили (пункт а)

Ответы

aboboskayaovrain 11.10.2020 15:55

Рассмотрим какое-нибудь число ; Пусть $\alpha$ - наибольшая степень десятки, которая делит ; Тогда можно представить в виде $10^{\alpha}\times y,\; 1\leq y\leq 9$ ; Это число имеет $\alpha+1$ цифру. Теперь $x^{2}=10^{2\alpha}y^{2},\; 1\leq y^{2}\leq 81$ ; Поэтому число $x^{2}$ имеет в своей записи не больше, чем $2\alpha+2$ цифры, но и не меньше, чем $2\alpha+1$ цифру.

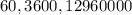Если взять первый случай, то пусть первое число ; Тогда второе число - $x^{2}$ , третье - $x^{4}$ ; Пусть у $\alpha$ цифр, а $y\geq 6$ ; Тогда у первого числа $\alpha$ цифр, у второго $2\alpha$ , у третьего $4\alpha$ . Итого $7\alpha$ цифр. Нас просят, чтоб их было 14. То есть $\alpha=2$ . Поэтому, учитывая ограничение на , можно взять x=60 ; Получим 60, 3600, 12 960 000 ;

Можно было поступить и иначе. Это видно из предыдущего примера. Пусть надо не 14, а 7 цифр. Небольшим перебором можно найти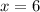 x=6 , а затем заметить, что его можно умножить на 10, тем самым увеличив количество цифр в 2 раза, т.е. до 14