Круг, квадрат и равносторонний треугольник равновелики. Найти отношение их периметров.

Пошаговое объяснение:

Равновелики - это значит с одинаковой площадью.

Площадь круга S=πR² 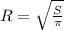 =>  , площадь квадрата S=a^2  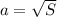=>  , площадь равностороннего треугольника -  =>  

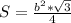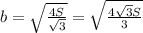
Периметр круга - это длина окружности, которой он ограничен: .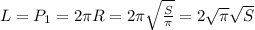

Периметр квадрата - это сумма длин всех его четырёх сторон: .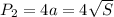

Периметр равностороннего треугольника - это сумма длин всех трёх его сторон: .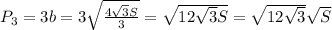

а теперь найдём отношение  :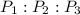

  =>        =>    

Последнее - и есть ответ

:)