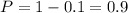Кпразднику было выпущено 1 лотерейных билетов, среди которых 100 выигрышных . фирма салют купила 200 билетов для своих сотрудников.
а) определите, какое распределение будет подходящей моделью в данном случае.
б) какова вероятность того, что среди купленных фирмой билетов окажется не более четырех выигрышных?
в) сколько билетов надо купить, чтобы среди них с вероятностью 90% оказался хотя бы один выигрышный?
Другие вопросы по теме Математика
Популярные вопросы
- Не понимаю, как написать изложение от 3-го лица текст: мама...
3 - Напишите сочинение на тему .используйте материалы дргих разделов...
2 - Решите полностью с поеснениями.в несколько школьных буфетах...
2 - Напишите сочинение на тему после 15...
2 - Равнобедренный треугольник авс, описанный вокруг круга. центр,...
3 - Решите неравенство: (x-0,3)(6x-1)(5-2x) 0...
1 - Ңқазіргі жағдайдағы ең басты мәселесі – ақша. написать эссе...
1 - Сочинение по плану анализу лирического произведения на тему...
2 - Когда отмечают праздник ивана купалы ночь с на...
2 - Что такое промыслы и какие они бывают ( в биологии)...
1
а) данная модель распределена по биномиальному закону.Вероятность успеха в одном испытании равна p = 100/10000 = 0.01, тогда q = 1 - p = 1 - 0.01 = 0.99
б) Вероятность того, что среди купленных фирмой билетов окажется не более четырех выигрышных, равна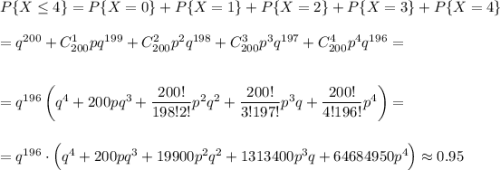
в) Воспользуемся вероятностью противоположного события.
Подсчитаем сколько нужно взять билетов, чтобы среди них с вероятность 100% - 90% = 10% оказались все не выигрышные билеты.
Откуда n = 230, так как вероятность того, что купленные билеты невыигрышные равна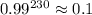 откуда вероятность того, что среди купленных билетов окажутся хотя бы один выигрышный билет равна
откуда вероятность того, что среди купленных билетов окажутся хотя бы один выигрышный билет равна