Кондрат последовательно заходит в 5 автобусов до тех пор, пока не нарвется на контролера, который и положит конец этим экспериментам. Если в пятом автобусе контролер не появляется, то Кондрат, довольный, идет обедать. Вероятность встретить контролера в любом автобусе 0,1. Найти математическое ожидание числа автобусов, в которые успеет зайти Кондрат.
Другие вопросы по теме Математика
Популярные вопросы
- А) -4/5 + (-5/6) = ? б) -3 целых 1/7 + (-1 целая 3/14) = ? в) -1 целая...
3 - Вопрос №3 ? В результате разложения воды электрическим током получили...
3 - Выписать из текста сказки пять примеров, обозначающих движение. Выписать...
1 - Таблица Производства аммиачной селитры подскажите...
3 - Перепишите предложение, исправив орфографические ошибки: с начальной...
2 - Сделайте 3 действие и объясните. Делать не много....
2 - Кончилась зима, зазеленела трава, и на деревьях распустились почки....
2 - На наведеній моделі молекули алкану сірим кружком позначенно атоми Карбону,...
1 - Ойнайық4. Көршіңмен бинго ойна.А оқушыӘ оқушы...
3 - What do the underlined words refer to she (line 1) her (line 4) he (line...
3
Пошаговое объяснение:
Пусть проводится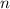 независимых испытаний, даже не обязательно повторных. И в каждом из которых случайное событие
независимых испытаний, даже не обязательно повторных. И в каждом из которых случайное событие 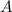 может появиться с вероятностью
может появиться с вероятностью 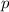 . Тогда случайная величина
. Тогда случайная величина 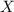 , это число появлений события
, это число появлений события 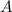 в данной серии испытаний, имеет биномиальное распределение.
в данной серии испытаний, имеет биномиальное распределение.
Кондрат последовательно заходит в 5 автобусов, то есть совершается серия и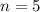 и только 5 похождений в различные автобусы, где вероятность встретить контролера в каждом из них составляет
и только 5 похождений в различные автобусы, где вероятность встретить контролера в каждом из них составляет 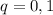 . Тогда вероятность НЕ встретить контролера в автобусе равна
. Тогда вероятность НЕ встретить контролера в автобусе равна 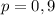 .
.
Математическое ожидание при биномиальном распределении рассчитывается согласно формуле:
Найдем математическое ожидание числа автобусов в которые успеет зайти Кондрат: