Комплект содержит 5 изделий первого сорта, 4 - второго и 3 изделия третьего сорта. найдите вероятность того, что два случайно взятые изделия

Question

Математика: Комплект содержит 5 изделий первого сорта, 4 - второго и 3 изделия третьего сорта. найдите вероятность того, что два случайно взятые изделия будут одного сорта.

4chanus · Answer

Вероятность того, что наугад выбранные два изделия будут первого сорта равна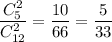 $\dfrac{C^2_5}{C^2_{12}}=\dfrac{10}{66}=\dfrac{5}{33}$ .

Вероятность того, что случайно выбранные изделия будут второго сорта равна, равна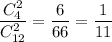 $\dfrac{C^2_4}{C^2_{12}}=\dfrac{6}{66}=\dfrac{1}{11}$

Вероятность того, что случайно выбранные изделия будут третьего сорта равна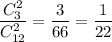 $\dfrac{C^2_3}{C^2_{12}}=\dfrac{3}{66}=\dfrac{1}{22}$

По теореме сложения, вероятность того, что два случайно взятые изделия будут одного сорта равна

$P=\dfrac{5}{33}+\dfrac{1}{11}+\dfrac{1}{22}=\dfrac{10+6+3}{66}=\dfrac{19}{66}$

Комплект содержит 5 изделий первого сорта, 4 - второго и 3 изделия третьего сорта. найдите вероятность того, что два случайно взятые изделия будут одного сорта.

Популярные вопросы