Коло задано рівнянням: (x - 3)2 + (y + 2)2 = 49.
Запишіть рівняння прямої, яка проходить через
центр заданого кола та точку К(7; 1). Знайдіть
кутовий коефіцієнт цієї прямої.
Другие вопросы по теме Математика
Популярные вопросы
- Кто такой телеграфист, коммивояжёр, лоцман, провизор, фитодизайнер , пекарь,...
2 - 1\25 + 1\40 не могу сосчитать сколько будет...
1 - Увинни пуха было 5 горшочков с липовым мёдом и 4 с цветочным,3 горшочка он...
1 - Представьте в виде многочлена выражение. 2x-(x-3)(x²+2)...
1 - Солнце ярко сияло в голубом небе словосочитания...
2 - Вчём смысл рассказа ричарда баха чайка по имени джонатан ливингстон ? рассказ...
2 - Вмагазине было 762 телевизора.в первый день было продано 40 телевизоров,во...
1 - Какое словосочетание подходит к местоимению нею...
1 - Водном элеваторе было зерна в 3 раза больше, чем в другом. из первого элеватора...
3 - Решить по генетике. черный цвет у собаки доминантный признак, коричневый цвет...
2
По виду уравнения окружности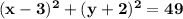
определяем центр окружности . Это точка Q( 3 ;-2 ) и радиус R=7 .
Прямая проходит через центр Q( 3 ; -2 ) и точку К( 7 ; 1) .
Запишем уравнение прямой KQ в виде y = kx + b .
Подставим координаты точек К и Q в уравнение , получим
Уравнение прямой KQ :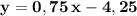 ,
,
угловой коэффициент k=0,75 .