Каждый ученик школы знает хотя бы одного другого, а любые двое, которые имеют поровну знакомых, общих знакомых не имеют. Доказать, что найдется школьник, у которого ровно один знакомый.
Другие вопросы по теме Математика
Популярные вопросы
- Ть будь ласка потрібен діалог на одну із тем 1. красиві слова і добрі...
2 - Сравните значения выражений i-5/18i*i-3/10i+7/12 и i-25/26i*-i26/75i*i-1i...
1 - Написать 3 чистушки про школу (небольшие)...
1 - Расположить буквы в правильном порядке оьслат...
3 - B) complete the following statements.native are those who speak a language...
1 - Решите неравенство (подробно)...
3 - Написать сказку в художественном виде...
3 - Как с разных видов искусства был отображен портрет александра невского?...
1 - Предложение с он босага и сол босага...
2 - 99 целое нечетное число начиная с 1...
2
Представим учеников и отношение знакомства в виде графа. Найдем вершину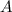 наибольшей степени
наибольшей степени 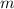 . Пусть вершина
. Пусть вершина 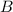 инцидентна
инцидентна 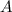 и имеет наибольшую степень
и имеет наибольшую степень 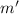 среди остальных вершин-соседей
среди остальных вершин-соседей 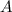 . Если
. Если 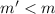 , то по принципу Дирихле найдутся две вершины с одинаковой степенью, а у них есть общая вершина —
, то по принципу Дирихле найдутся две вершины с одинаковой степенью, а у них есть общая вершина — 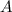 , противоречие. Поскольку
, противоречие. Поскольку 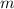 максимально, то
максимально, то 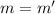 . Итак, у нас ровно
. Итак, у нас ровно 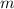 вершин, причем их степени различны и не превосходят
вершин, причем их степени различны и не превосходят 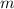 , следовательно, они пробегают все значения от
, следовательно, они пробегают все значения от  до
до 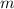 . Вершина степени
. Вершина степени  и является искомой.
и является искомой.