Какой вид имеет характеристическое уравнение для дифференциального уравнения y"+py'+qy=0 ?
Ответы
Собственно говоря, как вообще получается характеристическое уравнение - -функцию у заменяем на 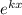 , затем находим производные нужных порядков, выносим
, затем находим производные нужных порядков, выносим 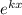 как общий множитель и решаем уравнение
как общий множитель и решаем уравнение
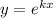
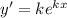
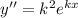
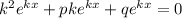
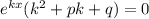
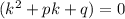 - вот такой вид имеет характеристическое уравнение для дифференциального уравнения y"+py'+qy=0
- вот такой вид имеет характеристическое уравнение для дифференциального уравнения y"+py'+qy=0
ПОКАЗАТЬ ОТВЕТЫ
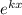 , затем находим производные нужных порядков, выносим
, затем находим производные нужных порядков, выносим 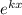 как общий множитель и решаем уравнение
как общий множитель и решаем уравнение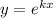
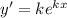
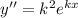
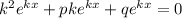
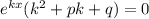
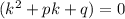 - вот такой вид имеет характеристическое уравнение для дифференциального уравнения y"+py'+qy=0
- вот такой вид имеет характеристическое уравнение для дифференциального уравнения y"+py'+qy=0
Другие вопросы по теме Математика
Популярные вопросы
- Какое влияние оказала биосфера на другие оболочки земли...
3 - Сочинение на тему почему геракла назвают героем . примерно 15...
3 - Как по тысяча семьсот семьдесят семь...
2 - Какие меры придпринимает человечество по защите окружающей среды...
2 - Если из первого кошелька взять 2 рубля, и положить во второй,...
3 - Превидите развернутые примеры гомологичных и аналогичных органов...
3 - На тело массой 500 г действуют две силы, направленные в противоположные...
2 - Какой самый большой и какой самый маленький океаны?...
2 - Вкаком соотношении масс соединяются кальций и кислород с образованием...
3 - Как восстановить потёртую бумагу? я лезвием оценку соскаблил...
3